Continuidad de una función
De Wikillerato
(Diferencias entre revisiones)
| Línea 13: | Línea 13: | ||
\mathrm{f} \left( \, x_0 \, \right) | \mathrm{f} \left( \, x_0 \, \right) | ||
</math>. | </math>. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<br/> | <br/> | ||
| Línea 41: | Línea 34: | ||
x, \, \forall x \in \left( \, a, \, b \, \right) | x, \, \forall x \in \left( \, a, \, b \, \right) | ||
</math>. | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \forall | ||
| + | </math> | ||
| + | es un simbolo matematico que significa '''''para todo'''''. | ||
<br/> | <br/> | ||
Revisión de 16:49 11 ago 2010
Tabla de contenidos |
Definiciones
Una funciónes continua en
si y solo si
.
Una función
 es continua en un intervalo
es continua en un intervalo
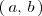 si y solo si
si y solo si
 es continua en
es continua en
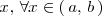 .
.
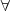 es un simbolo matematico que significa para todo.
es un simbolo matematico que significa para todo.
Se dice que una función
 es continua si y solo si es continua en cada
es continua si y solo si es continua en cada
 de su dominio.
de su dominio.
¿Donde es f continua?
Para determinar si una función
 es continua en
es continua en
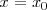 comprobaremos que se verifican todas y cada una de las condiciones siguientes:
comprobaremos que se verifican todas y cada una de las condiciones siguientes:
Condición 1.
Existe 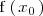 ,
es decir,
,
es decir,  esta en el dominio de
esta en el dominio de  .
.
Condición 2.
Existe 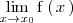 .
.
Condición 3.
Ambos, 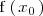 y
y 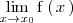 son iguales.
son iguales.
Ejercicios Resueltos
Continuidad y derivabilidad de una función
Continuidad y derivabilidad de una función definida a trozos



