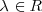Definición de una recta
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | + | Al igual que ocurre en el plano, una recta en el espacio queda determinada conociendo un | |
| + | punto | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | y un vector no nulo | ||
| + | <math> | ||
| + | \vec {\mathbf{v}} | ||
| + | </math> | ||
| + | que se llama vector director o direccional de la recta. | ||
| + | |||
| + | Estudiamos a continuacion las diferentes formas que puede adoptar la ecuacion de una | ||
| + | recta. | ||
| + | |||
| + | ==Ecuacion en forma vectorial== | ||
| + | |||
| + | La recta que pasa por el punto | ||
| + | <math> | ||
| + | P_0 = | ||
| + | \left( | ||
| + | \, x_0, \, y_0, \, z_0 \, | ||
| + | \right) | ||
| + | </math> | ||
| + | y tiene por vector director | ||
| + | <math> | ||
| + | \vec {\mathbf{v}} = | ||
| + | \left( | ||
| + | \, v_x, \, v_y, \, v_z \, | ||
| + | \right) | ||
| + | </math> | ||
| + | es el conjunto de puntos | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | del espacio que verifican la relacion vectorial | ||
| + | <math> | ||
| + | \stackrel{P_oP}{\longrightarrow} {} = \lambda \vec {\mathbf{v}} | ||
| + | </math> | ||
| + | con | ||
| + | <math> | ||
| + | \lambda \in R | ||
| + | </math> | ||
| + | | ||
| + | [[Imagen:Recta.gif]] | ||
Revisión de 18:59 30 nov 2006
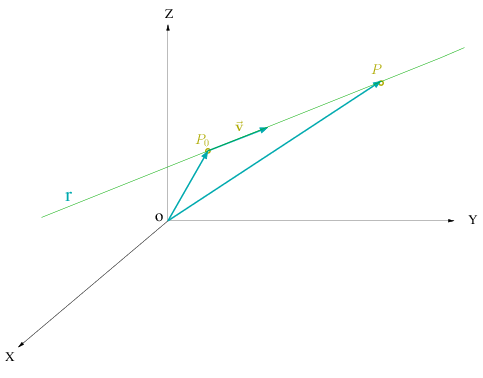
Al igual que ocurre en el plano, una recta en el espacio queda determinada conociendo un
punto
 y un vector no nulo
y un vector no nulo
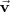 que se llama vector director o direccional de la recta.
que se llama vector director o direccional de la recta.
Estudiamos a continuacion las diferentes formas que puede adoptar la ecuacion de una recta.
Ecuacion en forma vectorial
La recta que pasa por el punto
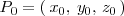 y tiene por vector director
y tiene por vector director
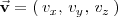 es el conjunto de puntos
es el conjunto de puntos
 del espacio que verifican la relacion vectorial
[Unparseable or potentially dangerous latex formula. Error 3 ]
con
del espacio que verifican la relacion vectorial
[Unparseable or potentially dangerous latex formula. Error 3 ]
con