Métodos de integración
De Wikillerato
(Página nueva: ==Integración por partes== <br/> La fórmula para la derivada de un producto es: <center> <math> \left( \, u \cdot v \, \right)^\prime = u^\prime \cdot v + u \cdot v^\prime </mat...) |
|||
| Línea 33: | Línea 33: | ||
</math> | </math> | ||
a partir de la integral | a partir de la integral | ||
| - | |||
<math> | <math> | ||
\int u^\prime \cdot v \cdot\mathrm{d}x | \int u^\prime \cdot v \cdot\mathrm{d}x | ||
| - | </math | + | </math>. |
| - | + | ||
<br/> | <br/> | ||
| Línea 43: | Línea 41: | ||
Para que sea de utilidad el utilizar este metodo es necesario que nos resulte | Para que sea de utilidad el utilizar este metodo es necesario que nos resulte | ||
mas sencilla de resolver la integral | mas sencilla de resolver la integral | ||
| - | |||
<math> | <math> | ||
\int u^\prime \cdot v \cdot\mathrm{d}x | \int u^\prime \cdot v \cdot\mathrm{d}x | ||
</math> | </math> | ||
| - | + | que la integral de partida, | |
| - | que la integral | + | |
| | ||
| - | |||
<math> | <math> | ||
\int u \cdot v^\prime \cdot \mathrm{d}x | \int u \cdot v^\prime \cdot \mathrm{d}x | ||
| - | </math | + | </math>. |
| - | + | ||
<br/> | <br/> | ||
| Línea 160: | Línea 154: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \frac{\mathrm{d}t}{ | + | \frac{\mathrm{d}t}{\mathrm{h}^\prime \left( t \right)} = \mathrm{d}x |
</math> | </math> | ||
</center> | </center> | ||
| + | Con este cambio de variable, la integral anterior se pondria de la der | ||
| - | + | [[Category: Matemáticas]] | |
| - | + | ||
| - | + | ||
Revisión de 15:22 15 nov 2010
Integración por partes
La fórmula para la derivada de un producto es:
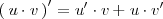
Despejando el último sumando, queda:
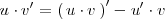
Si integramos en los dos miembros, se obtiene:
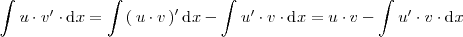
La última igualdad es cierta porque una primitiva de la derivada de una función es esa misma función.
Esta fórmula permite calcular la integral
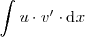 a partir de la integral
a partir de la integral
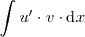 .
.
Para que sea de utilidad el utilizar este metodo es necesario que nos resulte
mas sencilla de resolver la integral
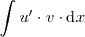 que la integral de partida,
que la integral de partida,
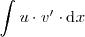 .
.
Ejemplo
Calculemos la integral
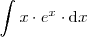
por partes.
Si hacemos
[Unparseable or potentially dangerous latex formula. Error 3 ]
se tiene que
[Unparseable or potentially dangerous latex formula. Error 3 ]
Utilizando la fórmula que hemos visto antes
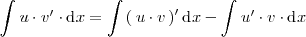
Por tanto
[Unparseable or potentially dangerous latex formula. Error 3 ]
Método de sustitución
Supongamos que queremos resolver una integral del tipo:
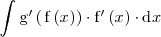
Una manera de resolver el problema es haciendo el cambio de variable
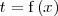
La nueva variable
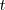 es una función de
es una función de
 ,
con lo cual podemos hablar de la derivada de
,
con lo cual podemos hablar de la derivada de
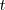 con respecto de
con respecto de
 , que se puede escribir como un cociente de diferenciales:
, que se puede escribir como un cociente de diferenciales:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Supongamos que existe una funcion
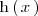 tal que
tal que
[Unparseable or potentially dangerous latex formula. Error 3 ]
Entonces, se tendria que:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Con este cambio de variable, la integral anterior se pondria de la der
Tweet


