Métodos de integración
De Wikillerato
| Línea 52: | Línea 52: | ||
<br/> | <br/> | ||
| - | ==Ejemplo== | + | ===Ejemplo=== |
<br/> | <br/> | ||
| Línea 97: | Línea 97: | ||
<math> | <math> | ||
\int x \cdot e^x \cdot \mathrm{d}x = x \cdot e^x - \int 1 \cdot e^x | \int x \cdot e^x \cdot \mathrm{d}x = x \cdot e^x - \int 1 \cdot e^x | ||
| - | \cdot\mathrm{d}x = x \cdot e^x - e^x = \left( \, x - 1 \, \right) \cdot e^x | + | \cdot\mathrm{d}x = x \cdot e^x - e^x + C = \left( \, x - 1 \, \right) \cdot e^x + C |
</math> | </math> | ||
</center> | </center> | ||
| Línea 212: | Línea 212: | ||
<br/> | <br/> | ||
| - | ==Ejemplo== | + | ===Ejemplo=== |
<br/> | <br/> | ||
| Línea 239: | Línea 239: | ||
\mathrm{f}^\prime \left( x \right) & = e^x | \mathrm{f}^\prime \left( x \right) & = e^x | ||
\\ | \\ | ||
| - | \int e^x \cdot \cos \left( \, e^x \, \right) \cdot \mathrm{d}x = \int | + | \int e^x \cdot \cos \left( \, e^x \, \right) \cdot \mathrm{d}x & = \int |
| - | \mathrm{g} \left( \, \mathrm{f} \left( x \right) \right) \cdot \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x | + | \mathrm{g} \left( \, \mathrm{f} \left( x \right) \right) \cdot \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x |
\end{array} | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
| - | En este caso, | + | En este caso, una primitiva de |
| - | + | <math> | |
| - | + | \mathrm{g} \left( x \right) | |
| + | </math> | ||
| + | es | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{G} \left( \, x \, \right) = \mathrm{sen} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | Por lo tanto | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
| + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \infty \mathrm{g} \left( | ||
| + | t \right) \cdot \mathrm{d}t = \mathrm{G} \left( t \right) + C= \mathrm{G} \left( | ||
| + | \mathrm{f} \left( x \right)\right) + C = \mathrm{sen} \left( e^x \right) + C | ||
| + | </math> | ||
| + | </center> | ||
[[Category: Matemáticas]] | [[Category: Matemáticas]] | ||
Revisión de 16:11 15 nov 2010
Tabla de contenidos[ocultar] |
Integración por partes
La fórmula para la derivada de un producto es:
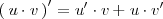
Despejando el último sumando, queda:
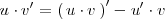
Si integramos en los dos miembros, se obtiene:
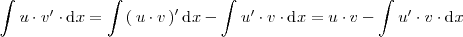
La última igualdad es cierta porque una primitiva de la derivada de una función es esa misma función.
Esta fórmula permite calcular la integral
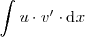 a partir de la integral
a partir de la integral
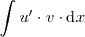 .
.
Para que sea de utilidad el utilizar este metodo es necesario que nos resulte
mas sencilla de resolver la integral
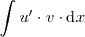 que la integral de partida,
que la integral de partida,
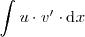 .
.
Ejemplo
Calculemos la integral
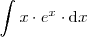
por partes.
Si hacemos
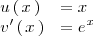
se tiene que
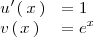
Utilizando la fórmula que hemos visto antes
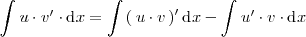
Por tanto
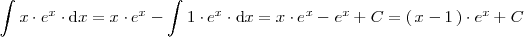
Método de sustitución
Supongamos que queremos resolver una integral del tipo:
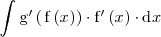
Una manera de resolver un problema de este tipo es haciendo el cambio de variable
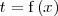
La nueva variable
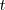 es una función de
es una función de
 ,
con lo cual podemos hablar de la derivada de
,
con lo cual podemos hablar de la derivada de
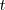 con respecto de
con respecto de
 , que se puede escribir como un cociente de diferenciales:
, que se puede escribir como un cociente de diferenciales:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Ambos miembros de la igualdad anterior son dos formas distintas de denotar la
derivada de la funci\'on
 .
.
Despejando
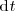 en la igualdad anterior, se deduce que
en la igualdad anterior, se deduce que
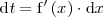
Sustituyendo
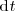 por
por
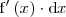 y
y
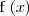 por
por
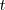 en
en
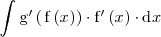
se tiene que
[Unparseable or potentially dangerous latex formula. Error 3 ]
Supongamos que [Unparseable or potentially dangerous latex formula. Error 3 ] es una primitiva de [Unparseable or potentially dangerous latex formula. Error 3 ], entonces
[Unparseable or potentially dangerous latex formula. Error 3 ]
Ejemplo
Calculemos mediante el método de sustitución la integral
[Unparseable or potentially dangerous latex formula. Error 3 ]
Para ello utilizamos las formulas dadas en la descripción del metodo de sustitución con
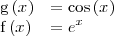
Observese que
[Unparseable or potentially dangerous latex formula. Error 3 ]
En este caso, una primitiva de
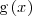 es
es
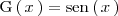
Por lo tanto
[Unparseable or potentially dangerous latex formula. Error 3 ]



