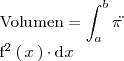Cálculo de áreas y volúmenes
De Wikillerato
| Línea 1: | Línea 1: | ||
<br/> | <br/> | ||
| - | ==Cálculo | + | ==Cálculo del área entre dos curvasmediante integrales== |
<br/> | <br/> | ||
| Línea 177: | Línea 177: | ||
<math> | <math> | ||
= \left| \, \frac{\left( \, -1 \, \right)^4}{4} - \frac{\left( \, -1 \, | = \left| \, \frac{\left( \, -1 \, \right)^4}{4} - \frac{\left( \, -1 \, | ||
| - | \right)^ | + | \right)^2}{2} - \left( \, \frac{\left( \, 0 \, \right)^4}{4} - \frac{\left( \, 0 \, |
| - | \right)^ | + | \right)^2}{2} \, \right) \right| + |
\left| \, \frac{\left( \, 0 \, \right)^4}{4} - \frac{\left( \, 0 \, | \left| \, \frac{\left( \, 0 \, \right)^4}{4} - \frac{\left( \, 0 \, | ||
| - | \right)^ | + | \right)^2}{2} - \left( \, \frac{\left( \, 1 \, \right)^4}{4} - \frac{\left( \, 1 \, |
| - | \right)^ | + | \right)^2}{2} \, \right) \right| = \frac{9}{4} |
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Volumen de un cuerpo de revolución== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Al girar un trozo de la grafica de una función | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right), \, \forall x \in \left[ \, a, \, b \, \right] | ||
| + | </math> | ||
| + | alrdedor del eje X se genera un cuerpo de revolución cuyo volumen | ||
| + | queremos calcular. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si dividimos el intervalo | ||
| + | <math> | ||
| + | \left[ \, a, \, b \, \right] | ||
| + | </math> | ||
| + | en | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | subintervalos iguales, entonces podemos aproximar el area del cuerpo de revolución | ||
| + | por | ||
| + | <center> | ||
| + | <math> | ||
| + | \sum_{i=1}^n \pi \ddot \mathrm{f}^2 \left( \, x_i \, \right) \cdot \left( \, x_i - x_{i-1} \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | donde | ||
| + | <math> | ||
| + | x_i | ||
| + | </math> | ||
| + | es el limite superior del i-esimo subintervalo. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El producto | ||
| + | <center> | ||
| + | <math> | ||
| + | \pi \ddot \mathrm{f}^2 \left( \, x_i \, \right) \cdot \left( \, x_i - x_{i-1} \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | es el volumen de un cilindro cuyo eje de simetria ( eje central ) es el eje X y | ||
| + | cuyas bases estan en los planos de ecuación | ||
| + | <math> | ||
| + | x = x_{i-1} | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | x = x_i | ||
| + | </math>, | ||
| + | <math> | ||
| + | respectivamente. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Notese que | ||
| + | <math> | ||
| + | x_i - x_{i-1} = \frac{b - a}{n} | ||
| + | </math> | ||
| + | y que | ||
| + | <math> | ||
| + | x_n = b, \, x_0 = a | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para cada | ||
| + | <math> | ||
| + | i = 1, \, 2, \, \ldots n | ||
| + | </math> | ||
| + | tenemos un cilindro, de tal manera que la suma de los volumenes de estos | ||
| + | cilindros es una aproximación al volumen del cuerpo de revolución que queremos | ||
| + | calcular. Cuando hacemos tender | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | a | ||
| + | <math> | ||
| + | \infty | ||
| + | </math> | ||
| + | obtenemos el volumen del cuerpo dense revolución que coicide con la siguiente integral | ||
| + | <center>. | ||
| + | <math> | ||
| + | \text{Volumen} = \int_a^b \pi \ddot \mathrm{f}^2 \left( \, x \, \right) \cdot \mathrm{d}x | ||
</math> | </math> | ||
</center> | </center> | ||
Revisión de 12:42 25 dic 2010
Cálculo del área entre dos curvasmediante integrales
Supongamos que nos dan dos funciones
 y
y
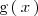 y nos piden calcular el área comprendida entre las graficas de ambas
funciones.
y nos piden calcular el área comprendida entre las graficas de ambas
funciones.
El area que nos piden coincide con el área comprendida entre la función
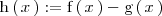 y el eje X.
y el eje X.
Para calcular el área comprendida entre la función
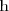 y el eje X, procedemos de la siguiente manera:
y el eje X, procedemos de la siguiente manera:
- 1. En primer lugar resolvemos la ecuación:
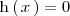
para obtener
 soluciones
soluciones 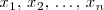 con
con
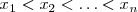
- 2 Buscamos una primitiva
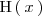 de
de
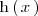 .
.
- 3. Llegados a este punto ya podemos calcular el área que nos piden con la
fórmula:

donde
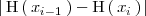
es el area comprendida entre las rectas verticales de ecuaciones
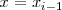 ,
,
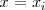 ,
el eje X y la grafica de la función
,
el eje X y la grafica de la función
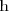 .
.
Ejemplo
Calculemos el área comprendida entre las graficas de
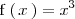 y
y
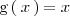 .
.
El area que nos piden coincide con el área comprendida entre la función
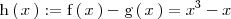 y el eje X.
y el eje X.
Para calcular el área comprendida entre la función
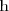 y el eje X, procedemos de la siguiente manera:
y el eje X, procedemos de la siguiente manera:
- 1. En primer lugar resolvemos la ecuación:
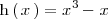
para obtener 3 soluciones
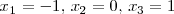 .
.
- 2 Una primitiva
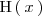 de
de 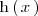 es
es
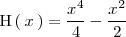
- 3. Llegados a este punto ya podemos calcular el área que nos piden:
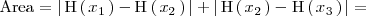
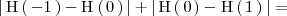
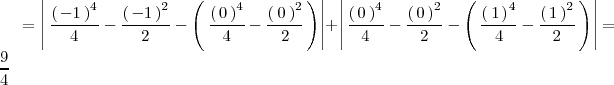
Volumen de un cuerpo de revolución
Al girar un trozo de la grafica de una función
![\mathrm{f} \left( \, x \, \right), \, \forall x \in \left[ \, a, \, b \, \right]
\mathrm{f} \left( \, x \, \right), \, \forall x \in \left[ \, a, \, b \, \right]](/images/math/math-16e6efe33eb08467bd9b5768863df5ed.png) alrdedor del eje X se genera un cuerpo de revolución cuyo volumen
queremos calcular.
alrdedor del eje X se genera un cuerpo de revolución cuyo volumen
queremos calcular.
Si dividimos el intervalo
![\left[ \, a, \, b \, \right]
\left[ \, a, \, b \, \right]](/images/math/math-bd2e5d8941aab87895e8817c63d00863.png) en
en
 subintervalos iguales, entonces podemos aproximar el area del cuerpo de revolución
por
subintervalos iguales, entonces podemos aproximar el area del cuerpo de revolución
por
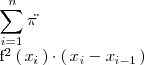
donde
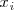 es el limite superior del i-esimo subintervalo.
es el limite superior del i-esimo subintervalo.
El producto
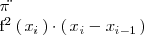
es el volumen de un cilindro cuyo eje de simetria ( eje central ) es el eje X y cuyas bases estan en los planos de ecuación
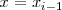 y
y
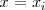 ,
,
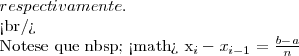 y que
y que
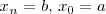 .
.
Para cada
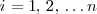 tenemos un cilindro, de tal manera que la suma de los volumenes de estos
cilindros es una aproximación al volumen del cuerpo de revolución que queremos
calcular. Cuando hacemos tender
tenemos un cilindro, de tal manera que la suma de los volumenes de estos
cilindros es una aproximación al volumen del cuerpo de revolución que queremos
calcular. Cuando hacemos tender
 a
a
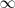 obtenemos el volumen del cuerpo dense revolución que coicide con la siguiente integral
obtenemos el volumen del cuerpo dense revolución que coicide con la siguiente integral
. Tweet