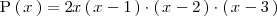La divisibilidad en los polinomios
De Wikillerato
| Línea 206: | Línea 206: | ||
\mathrm{P} \left( \, x \, \right) | \mathrm{P} \left( \, x \, \right) | ||
</math> | </math> | ||
| - | | + | sea 1. |
<br/> | <br/> | ||
| Línea 235: | Línea 235: | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
| - | |||
| - | |||
<br/> | <br/> | ||
| Línea 334: | Línea 332: | ||
<br/> | <br/> | ||
| - | + | intentamos encontrar las raices reales del polinomio | |
| - | + | ||
<math> | <math> | ||
| - | \mathrm{P} \ | + | \mathrm{P} |
| + | </math> | ||
| + | evaluandolo | ||
| + | en cada uno de los divisores de | ||
| + | <math> | ||
| + | \frac{a_0}{a_n} | ||
</math>. | </math>. | ||
<br/> | <br/> | ||
| - | <math> \mathrm{P} \left( \, a \, \right) = 0 </math> si y solo si <math> x - a </math> es | + | <math> \mathrm{P} \left( \, a \, \right) = 0 </math> si y solo si <math> x - a </math> es divisor de <math> \mathrm{P} \left( \, x \, \right) </math>. |
| + | |||
| + | <br/> | ||
| + | |||
| + | Asi, si hemos encontrado racies | ||
| + | <math> | ||
| + | r_1, r_2, \ldots r_n | ||
| + | </math> | ||
| + | del polinomio | ||
| + | <math> | ||
| + | \mathrm{P} | ||
| + | </math>, | ||
| + | entonces existe un polinomio | ||
| + | <math> | ||
| + | \mathrm{Q} | ||
| + | </math> | ||
| + | tal que | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{P} \left( \, x \, \right) = \left( \, x - r_1 \, \right) \cdot | ||
| + | \left( \, x - r_2 \, \right) \cdot \ldots \cdot \left( \, x - r_n \, \right) | ||
| + | \cdot \mathrm{Q} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| Línea 435: | Línea 460: | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
| - | |||
| - | |||
Revisión de 12:41 28 dic 2010
%% {{{ =la divisibilidad en los polinomios
Tabla de contenidos |
Definición de polinomio DIVISIBLE por otro
Un polinomio
 es divisible por otro polinomio
es divisible por otro polinomio
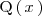 cuando existe otro polinomio
cuando existe otro polinomio
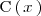 tal que
tal que
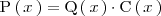
Los polinomios
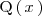 y
y
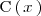 se llaman divisores de
se llaman divisores de
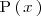 .
.
Ejemplo
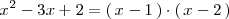
Por lo tanto, el polinomio
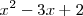 es divisible por los polinomios
es divisible por los polinomios
 y
y
 ,
o dicho de otra manera, los polinomios
,
o dicho de otra manera, los polinomios
 y
y
 son divisores del polinomio
son divisores del polinomio
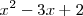 .
.
Definición de polinomio IRREDUCIBLE
Un polinomio
 de grado
de grado
 se dice que es irreducible cuando ningún polinomio de grado
menor que
se dice que es irreducible cuando ningún polinomio de grado
menor que
 y mayor que 0 es divisor de
y mayor que 0 es divisor de
 .
.
Cualquier polinomio que no sea irreducible se puede descomponer en forma de producto de polinomios irreducibles.
Ejemplos
Los siguientes dos polinomios son irreducibles:
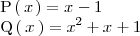
Factorización de polinomios
Por factorización de un polinomio se entiende su descomposición en forma de producto de polinomios irreducibles.
Ejemplo
Una descomposición del polinomio
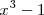 en producto de polinomios irreducibles es
en producto de polinomios irreducibles es
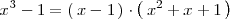
Otra posible descomposición del polinomio
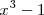 en producto de polinomios irreducibles es
en producto de polinomios irreducibles es
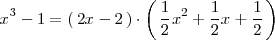
De hecho, hay infinitas descomposiciones posibles. Para cualquier número real
 distinto de 0, se tiene que
distinto de 0, se tiene que
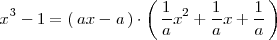
Simplificación de fracciones algebraicas
Una fracción algebraica es el cociente de dos polinomios. Para simplificar una fracción algebraica se divide los polinomios en el numerador y en el denominador por su maximo común divisor. Para encontrar el maximo común divisor de ambos polinomios se ha de factorizar previamente ambos. El proceso es analogo al que se seguiria en el caso de calcular el maximo común divisor de dos números naturales.
En el proceso de descomposición de ambos polinomios es conveniente que los
polinomios irreducibles de la descomposición se elijan de manera que si
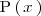 es un polinomio irreducible de grado
es un polinomio irreducible de grado
 obtenido en la factorización de un polinomio,
entonces el coeficiente que multiplica a
obtenido en la factorización de un polinomio,
entonces el coeficiente que multiplica a
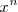 en
en
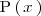 sea 1.
sea 1.
De esta manera se identifica mejor que polinomios irreducibles son divisores comunes de ambos polinomios ( el polinomio del numerador y el polinomio del denominador ).
Ejemplo
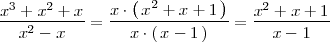
El maximo común divisor de los polinomios en el denominador y en el numerador es,
en este caso,
 .
.
Procedimiento para factorizar un polinomio
1. Sacamos  factor común, si ello es posible, y tantas veces
como se pueda.
factor común, si ello es posible, y tantas veces
como se pueda.
2. Si el polinomio
 es de grado dos:
es de grado dos:
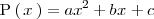
resolvemos la ecuación
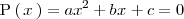
Si esta ecuación no tiene solución, el polinomio
 es irreducible,
pero si la ecuación anterior tiene soluciones
es irreducible,
pero si la ecuación anterior tiene soluciones
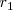 y
y
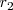 ,
entonces podemos factorizar
,
entonces podemos factorizar
 de la siguiente manera:
de la siguiente manera:
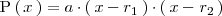
Puede ocurrir que
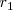 y
y
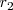 coincidan ( sean iguales ).
coincidan ( sean iguales ).
Si el polinomio
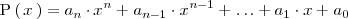
• es de grado mayor que dos
• sus coeficientes son enteros, y
•
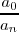 es un número entero
es un número entero
intentamos encontrar las raices reales del polinomio
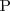 evaluandolo
en cada uno de los divisores de
evaluandolo
en cada uno de los divisores de
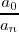 .
.
si y solo si
es divisor de
.
Asi, si hemos encontrado racies
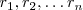 del polinomio
del polinomio
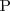 ,
entonces existe un polinomio
,
entonces existe un polinomio
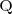 tal que
tal que
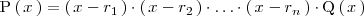
Ejemplo
Factorizemos el polinomio:
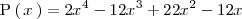
Como se puede sacar un
 factor común, eso es lo primero que hacemos:
factor común, eso es lo primero que hacemos:
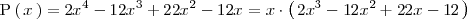
A continuación factorizamos
[Unparseable or potentially dangerous latex formula. Error 3 ]
Como se trata de un polinomio de grado mayor que dos, utilizamos la regla de Ruffini para ver
si podemos encontrar alguna de sus raices. Los candidatos a raiz que
consideramos son los divisores de
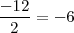 ,
que son
,
que son
[Unparseable or potentially dangerous latex formula. Error 3 ]
De este modo, se puede obtener que 3 es una raiz de
 ,
es decir,
,
es decir,
[Unparseable or potentially dangerous latex formula. Error 3 ]
y que
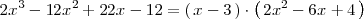
Finalmente, factorizamos el polinomio
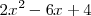
resolviendo la ecuación
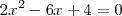
cuyas soluciones son 2 y 1, de manera que
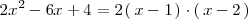
y, por tanto