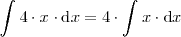Propiedades de las integrales indefinidas
De Wikillerato
(Diferencias entre revisiones)
(→Propiedad 2) |
m (Revertidas las ediciones realizadas por 83.55.228.177 (Talk); a la última edición de Fjmolina) |
||
| Línea 32: | Línea 32: | ||
\, = \, | \, = \, | ||
\int \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x \, + \, | \int \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x \, + \, | ||
| - | \int \mathrm{ | + | \int \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x |
</math> | </math> | ||
</center> | </center> | ||
Revisión de 09:45 20 ene 2011
Tabla de contenidos |
Propiedad 1
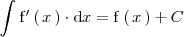
Propiedad 2
La integral de la suma de dos funciones es igual a la suma de las integrales de dichas funciones:
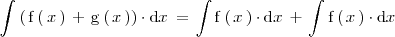
Ejemplo
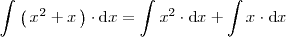
Propiedad 3
La integral indefinida del producto de un número realpor una función
es igual al producto de
por la integral indefinida de
:
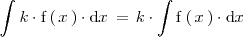
Ejemplo