Ejercicios:Ejercicio 1 (1)
De Wikillerato
(Diferencias entre revisiones)
(Página nueva: Se consideran las matrices <math> \mathbf{A} = \left( \begin{array}{ccc} 1 & 2 & \alpha \\ 1 & -1 & -1 \end{array} \right) </math> y <mat...) |
|||
| Línea 24: | Línea 24: | ||
# Encontrar los valores de <math>\alpha</math> para los que <math>AB </math> es [[Matriz inversa|invertible]]. | # Encontrar los valores de <math>\alpha</math> para los que <math>AB </math> es [[Matriz inversa|invertible]]. | ||
# Encontrar los valores de <math>\alpha</math> para los que <math>BA</math> es [[Matriz inversa|invertible]]. | # Encontrar los valores de <math>\alpha</math> para los que <math>BA</math> es [[Matriz inversa|invertible]]. | ||
| - | # Dados <math> | + | # Dados <math>a</math> y <math>b</math>, números reales cualesquiera, ¿puede ser el sistema |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
Revisión actual
Se consideran las matrices 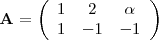 y
y 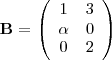 donde
donde 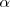 es un número real.
es un número real.
- Encontrar los valores de
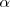 para los que
para los que 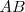 es invertible.
es invertible.
- Encontrar los valores de
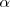 para los que
para los que 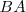 es invertible.
es invertible.
- Dados
 y
y 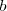 , números reales cualesquiera, ¿puede ser el sistema
, números reales cualesquiera, ¿puede ser el sistema
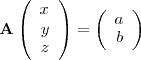 compatible determinado?
compatible determinado?



