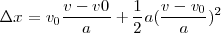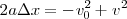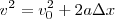Movimiento rectilíneo
De Wikillerato
(→Movimiento rectilíneo uniformemente acelerado) |
(→Movimiento rectilíneo uniformemente acelerado) |
||
| Línea 59: | Línea 59: | ||
con lo cual | con lo cual | ||
| - | <math> x = x_0 + \frac { 2 v_0 }{2} t +\frac {a t }{ 2 } t < | + | <math> x = x_0 + \frac { 2 v_0 }{2} t +\frac {a t }{ 2 } t </math> |
| - | <math> x = x_0 + v_0 t +\frac {1}{2} a t^2 < | + | <math> x = x_0 + v_0 t +\frac {1}{2} a t^2 </math> |
Como vemos, la ecuación obtenida para el espacio recorrido en un instante <math>t</math> es uns función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad. | Como vemos, la ecuación obtenida para el espacio recorrido en un instante <math>t</math> es uns función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad. | ||
Revisión de 16:32 18 dic 2006
Movimiento rectilíneo y uniforme
Llamamos así al movimiento de un punto material que recorre espacios iguales en tiempos iguales. Dado que hemos definido la velocidad como la variación del vector posición con relación al tiempo, en este tipo de movimiento la velocidad será constante:
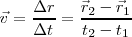
En el caso unidimensional, si queremos establecer la ecuación que nos dé la posición del punto material,  , en un instante cualquiera
, en un instante cualquiera  , sabiendo que la posición inicial es
, sabiendo que la posición inicial es 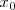 para el instante
para el instante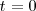 , tendremos:
, tendremos:
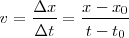
de donde,
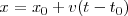
Vemos que obtenemos para  una función lineal de
una función lineal de  , en la cual v es el coeficiente de la variable independiente
, en la cual v es el coeficiente de la variable independiente  y
y 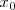 es la abcisa para el instante
es la abcisa para el instante 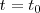 .
.
Movimiento rectilíneo uniformemente acelerado
Se ha denominado de este modo a aquel movimiento que describe una partícula de modo que son constantes las variaciones del vector velocidad en la unidad de tiempo, es decir aquel cuya aceleración permanece constante.
Dado que la velocidad no permanece constante pero si sus variaciones podremos escribir:
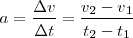
Si consideramos que en un instante cualquiera  el móvil lleva una velocidad
el móvil lleva una velocidad  , y fue
, y fue 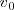 la velocidad con la que inició el movimiento, es decir la que tuvo en el instante
la velocidad con la que inició el movimiento, es decir la que tuvo en el instante 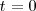 , tendremos:
, tendremos:
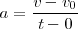
o lo que es igual
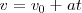
obteniendo para la velocidad una función lineal de  en la cual es la aceleración a el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a
en la cual es la aceleración a el coeficiente de la variable. Al representar la recta obtenida tendremos en cuenta que su pendiente igual a 
Por otra parte, podremos calcular la velocidad media 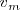 de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
de la partícula dividiendo el espacio total recorrido por el tiempo empleado en recorrerlo, es decir:
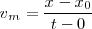
y por lo tanto
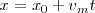
Por otra parte, dado que las variaciones de la velocidad son directamente proporcionales al tiempo, podremos escribir para la velocidad media:
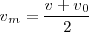
y sustituyendo en la ecuación precedente:
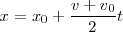
Sustituyendo v por su valor en función de la aceleración y del tiempo:
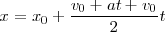
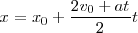
con lo cual
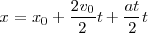
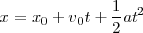
Como vemos, la ecuación obtenida para el espacio recorrido en un instante  es uns función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad.
es uns función del cuadrado del tiempo, y su representación gráfica en función del tiempo será una parábola, cuya tangente en cada punto tendrá por pendiente el valor de la velocidad.
Si eliminamos el tiempo entre las ecuaciones de la velocidad y del espacio:
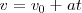
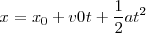
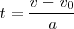
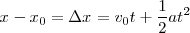
sustituyendo  por el valor obtenido en la ecuación de la velocidad
por el valor obtenido en la ecuación de la velocidad