Métodos de resolución de sistemas de ecuaciones lineales

De Wikillerato

(Diferencias entre revisiones)

Revisión de 17:03 24 abr 2013

Tabla de contenidos

1 Introducción
2 Método de reducción
3 Método de igualación
4 Método de sustitución
5 Método de Gauss
6 Método de la matriz inversa
7 Regla de Cramer
- 7.1 Ejemplo

Introducción

Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones.

Los métodos de igualación, sustitución y reducción consisten en encontrar y resolver, para cada una de las incognitas, una ecuación con esa incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas facil, ¿no?).

A estas ecuaciones, con solo una incognita, se llega a traves de una serie de pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos incognitas que las ecuaciones previas.

Así, es posible que en uno de estos pasos de eliminación de incognitas se utilize un método ( el de reducción, por ejemplo ) y que, en el siguiente paso, se utilize otro método ( el de igualación, por ejemplo ).

Cada vez que se encuentra la solución para una incognita, se sustituye esta incognita por su solución para obtener asi ecuaciones con menos incognitas.

Los métodos de igualación, sustitución, reducción y Gauss se pueden utilizar para resolver sistemas de ecuaciones compatibles determinados e indeterminados.

Estos mismos métodos tambien pueden utilizarse para comprobar si un sistema de ecuaciones es compatible o no. La utilizacion de cualquiera de ellos conduciria, en el caso de que el sistema fuese incompatible, a una igualdad que es falsa, por ejemplo:

$2 = 3$

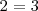
El método de la matriz inversa y la regla de Cramer solo se pueden utilizar en el caso de que el sistema de ecuaciones lineales sea compatible determinado.

Método de reducción

Ola ke ase?

Método de igualación

Método de sustitución

Método de Gauss

Método de la matriz inversa

Un sistema de ecuaciones lineales se puede escribir en forma matricial:

$\mathbf{A} \cdot \mathbf{X} \, = \, \mathbf{B}$

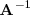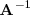Si $\mathbf{A}^{-1}$ existe, es decir, si $\mathbf{A}$ es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda la igualdad anterior por la izquierda por $\mathbf{A}^{-1}$ , para obtener:

$\mathbf{X} \, = \, \mathbf{A}^{-1} \cdot \mathbf{B}$

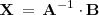
que es la solución del sistema de ecuaciones lineales de matriz de coeficientes $\mathbf{A}$ y matriz de terminos independientes $\mathbf{B}$ .

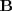Regla de Cramer

Gabriel Cramer nacio Ginebra ( Suiza ) 1704 y murio en 1752. A él le debemos la regla que lleva su nombre. ¡Gracias Gabriel por tu contribución a las Matemáticas!

Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede utilizar cuando la matriz $\mathbf{A}$ de coeficientes del sistema es cuadrada y de determinante no nulo. El que $\mathbf{A}$ sea cuadrada significa que el numero de incognitas y el numero de ecuaciones coincide.

Cuando el sistema de ecuaciones

$\left. <pre> \begin{array}{c} a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1 \\ a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2 \\ \dotfill \\ a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m \end{array} </pre> \right\}$

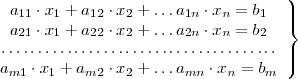
satisface las condiciones arriba mencionadas, su solución viene dada por:

$x_1 \, = \, \frac { <pre> \left| \begin{array}[c]{cccc} b_1 & a_{12} & \ldots & a_{1n} \\ b_2 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_m & a_{m2} & \ldots & a_{mn} \end{array} \right| </pre> } {|\mathbf{A}|} , \qquad \qquad x_2 \, = \, \frac { <pre> \left| \begin{array}[c]{cccc} a_{11} & b_1 & \ldots & a_{1n} \\ a_{21} & b_2 & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & b_m & \ldots & a_{mn} \end{array} \right| </pre> } {|\mathbf{A}|}, \qquad \qquad \ldots \ldots$

$\ldots \ldots, \qquad \qquad x_n \, = \, \frac { <pre> \left| \begin{array}[c]{cccc} a_{11} & a_{12} & \ldots & b_1 \\ a_{21} & a_{22} & \ldots & b_2 \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & b_m \end{array} \right| </pre> } {|\mathbf{A}|} \qquad \qquad$

En general

$x_i \, = \, \frac{|\mathbf{A}_i|}{|\mathbf{A}|}$

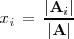
donde 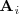$\mathbf{A}_i$ es la matriz que se obtiene sustituyendo la i-esima columna de $\mathbf{A}$ por la matriz de los terminos independientes, $B$ .

Ejemplo

Consideremos el sistema de ecuaciones:

$\left\{ <pre> \begin{array}[c]{rcl} x \, + \, y \, = \, 2 \\ x \, - \, y \, = \, 0 \end{array} </pre> \right.$

En este sistema de ecuaciones lineales, la matriz $\mathbf{A}$ de los coeficientes es una matriz cuadrada y $|\mathbf{A}| \, = \, \left| <pre> \begin{array}[c]{cc} 1 & ~~1 \\ 1 & -1 \end{array} </pre> \right| <pre>\, = \, -2 \neq 0 </pre> $ . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:

$x \, = \, \frac { <pre> \left| \begin{array}[c]{cc} 2 & ~~1 \\ 0 & -1 \end{array} \right| </pre> } {|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1 \qquad \qquad y \, = \, \frac { <pre> \left| \begin{array}[c]{cc} 1 & 2 \\ 1 & 0 \end{array} \right| </pre> } {|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1$