Trapecios
De Wikillerato
(→Propiedad 2) |
|||
| Línea 25: | Línea 25: | ||
En esta propiedad nos basamos para '''construir un trapecio cuando se conocen sus bases y sus diagonales: ''' se dibuja la base mayor '''AB''' y se le suma la menor '''CD'''. Se dibuja el triángulo de lados la suma de las bases '''AE''' y las diagonales '''AC''' y '''BD''' del trapecio. Así se halla '''C.''' | En esta propiedad nos basamos para '''construir un trapecio cuando se conocen sus bases y sus diagonales: ''' se dibuja la base mayor '''AB''' y se le suma la menor '''CD'''. Se dibuja el triángulo de lados la suma de las bases '''AE''' y las diagonales '''AC''' y '''BD''' del trapecio. Así se halla '''C.''' | ||
| - | Se trazan arcos de centro en C y radio CD y de centro en A y radio AD en cuya intersección está el punto D | + | Se trazan arcos de centro en C y radio CD y de centro en A y radio AD en cuya intersección está el punto D. |
[[Imagen:DibujoTecnico_I-3_30.gif]] | [[Imagen:DibujoTecnico_I-3_30.gif]] | ||
Revisión de 10:40 10 jun 2013
Los trapecios son cuadriláteros convexos con un par de lados paralelos a los que llamamos bases. Sus diagonales nunca se cortan en el punto medio. Solamente son inscriptibles los trapecios isósceles, que son los que tienen los dos lados no paralelos iguales.
Tabla de contenidos |
Propiedades y trazados generales
Propiedad 1
Si trazamos una paralela a un lado por un extremo de la base menor, el trapecio queda dividido en un paralelogramo cuyos lados son la base menor y dicho lado y en un triángulo cuyos lados son la diferencia de las bases y los dos lados del polígono.
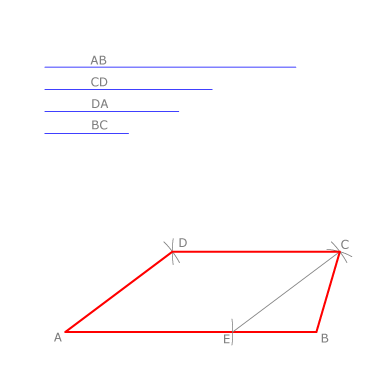
En esta propiedad nos basamos para construir un trapecio cuando se conocen sus bases y sus lados: se dibuja la base mayor AB y se le resta la menor CD. Se dibuja el triángulo de lados la diferencia de las bases EB y los lados AD y BC del trapecio. Así se halla C.
Se trazan arcos de centro en C y radio CD y de centro en A y radio AD en cuya intersección está el punto D.
Propiedad 2
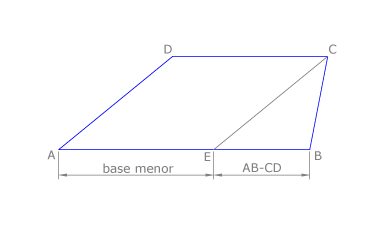
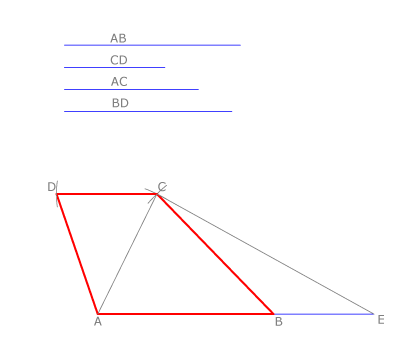
Si trazamos una paralela a una diagonal por un extremo de la base menor y dibujamos la base menor a continuación de la mayor se forma un triángulo cuyos lados son la suma de las bases y las dos diagonales del polígono.
En esta propiedad nos basamos para construir un trapecio cuando se conocen sus bases y sus diagonales: se dibuja la base mayor AB y se le suma la menor CD. Se dibuja el triángulo de lados la suma de las bases AE y las diagonales AC y BD del trapecio. Así se halla C.
Se trazan arcos de centro en C y radio CD y de centro en A y radio AD en cuya intersección está el punto D.
Propiedad 3
En los trapecios se llama altura a la distancia entre las bases.
Propiedad 4
Si se prolongan los lados de un trapecio se forma un triángulo que tiene en común con el trapecio un lado, la base mayor y los ángulos apoyados sobre ella.
Triángulo equivalente a un trapecio
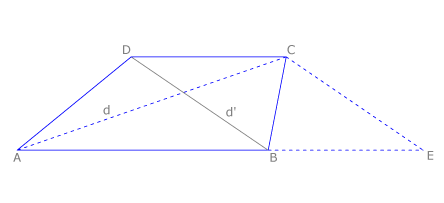
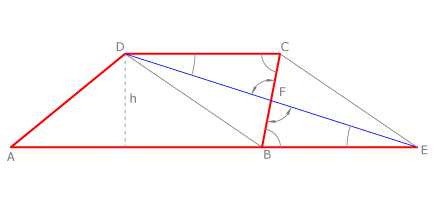
Todo trapecio es equivalente a un triángulo que tenga como base la suma de las bases y como altura respecto de ella la misma altura del trapecio.
En general se considera altura del trapecio a la distancia entre las bases.
Vamos a comprobarlo gráficamente. En la figura consideramos el trapecio ABCD y el triángulo ADE. Vemos que tienen una parte común, el cuadrilátero ABFD.
Por lo tanto bastará con comprobar que los triángulos FBE y DCF son iguales, lo que es evidente: DC=BE, CF=FB y DF=FE, por ser BECD un paralelogramo.
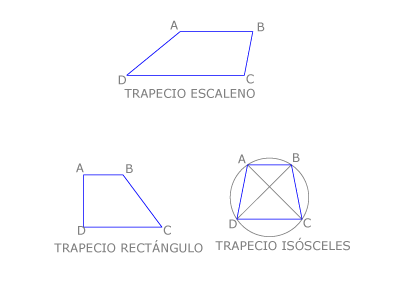
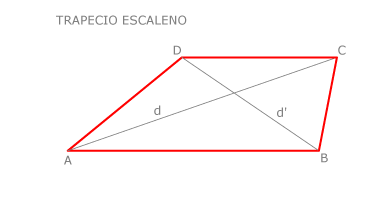
El trapecio escaleno
Sus lados, sus bases, sus diagonales y sus ángulos son desiguales.
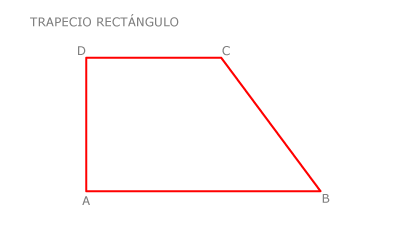
El trapecio rectángulo
Tiene dos ángulos rectos.
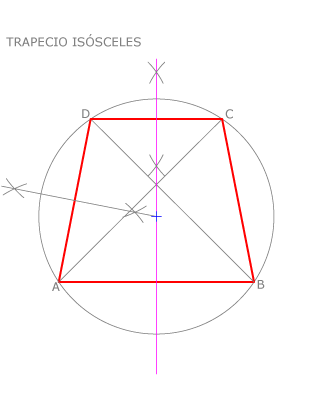
El trapecio isósceles
Tiene los lados iguales, lo que implica que tenga iguales las diagonales.
Tiene los ángulos iguales dos a dos, siendo iguales los ángulos que se apoyan en la misma base. Este trapecio tiene un eje de simetría y es inscriptible, ya que sus ángulos opuestos son suplementarios.
Tweet