Ángulos
De Wikillerato
(SHzTqDvzNkVbYXQsTK) |
|||
| Línea 1: | Línea 1: | ||
| - | + | ===Definición=== | |
| + | |||
| + | Un ángulo <math>\alpha</math> es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo. | ||
| + | |||
| + | [[Imagen:03Angulos.gif]] | ||
| + | |||
| + | ===Nomenclatura de los ángulos=== | ||
| + | Cuando un ángulo es menor de 90º se llama '''agudo''', si es mayor de 90º se llama '''obtuso''' y si mide 90º se llama '''recto'''. | ||
| + | El ángulo '''llano''' o '''extendido''' mide 180º, el ángulo completo 360º y el ángulo '''nulo''' 0º. | ||
| + | Dos ángulos se llaman '''suplementarios''' si suman 180º y '''complementarios''' si suman 90º. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 19.gif]] | ||
| + | |||
| + | Un ángulo '''cóncavo''' mide más de 180º grados. Si se prolonga el lado de un ángulo cóncavo la prolongación divide al ángulo. | ||
| + | Un ángulo '''convexo''' mide menos de 180º. Aunque se prolonguen sus lados las prolongaciones no dividen el ángulo. | ||
| + | Cuando dos rectas se cortan forman cuatro ángulos iguales dos a dos y suplementarios dos a dos. Los que son iguales son '''opuestos al vértice'''. | ||
| + | Dos ángulos son '''consecutivos''' cuando tienen un lado común. | ||
| + | Dos ángulos son '''adyacentes''' cuando son consecutivos y suplementarios. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 20.gif]] | ||
| + | |||
| + | Cuando una recta corta a dos rectas paralelas se forman ángulos que tienen las siguientes características: | ||
| + | |||
| + | Todos tienen un lado común y otro lado en rectas paralelas entre sí. | ||
| + | Hay ángulos que son iguales por ser '''opuestos al vértice''', como <math>\alpha</math> y <math>\delta \ </math>; otros ángulos iguales se llaman '''alternos internos''', como <math>\delta \ </math> y <math>\lambda</math> o alternos externos, como <math>\alpha</math> y <math>\pi \ </math>. | ||
| + | |||
| + | ===Propiedad relativa a los ángulos=== | ||
| + | |||
| + | Si se trazan dos rectas perpendiculares a los lados de un ángulo, éstas forman un ángulo igual al dado y otro suplementario. | ||
| + | Si se trazan dos rectas paralelas a los lados de un ángulo éstas forman un ángulo igual al dado y otro suplementario. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 21.gif]] | ||
| + | |||
| + | ===Traslado de un ángulo=== | ||
| + | |||
| + | Si queremos dibujar un ángulo igual a uno dado con vértice en un punto dado A, dibujamos un arco de radio arbitrario con centro en el vértice del ángulo dado y otro arco igual con centro en A. Medimos con el compás el arco limitado por los lados del ángulo dado y llevamos tal medida con el compás sobre el arco de centro en A. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 22.gif]] | ||
| + | |||
| + | ===Bisectriz de un ángulo=== | ||
| + | |||
| + | Es la recta que divide un ángulo en dos partes iguales. La propiedad de cada uno de los puntos de una bisectriz es que equidista de los lados del ángulo. | ||
| + | Para trazar una bisectriz se dibuja un arco de radio arbitrario con centro en el vértice. Este arco corta a los lados en los puntos '''M''' y '''N'''. La bisectriz b es la mediatriz de la cuerda '''MN'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 24.gif]] | ||
| + | |||
| + | Bisectriz de dos rectas que se cortan fuera del dibujo. | ||
| + | Vamos a resolver este problema por dos métodos: | ||
| + | |||
| + | 1. Dibujamos dos rectas '''r’ y s’''' paralelas a las dadas, '''r y s''', de modo que la distancia '''d''' entre los dos pares de paralelas sea la misma. | ||
| + | |||
| + | La bisectriz '''b''' buscada es la bisectriz de '''r’ y s’'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 25.gif]] | ||
| + | |||
| + | 2. Dibujamos un segmento arbitrario '''MN''' que tenga un extremo en cada una de las rectas dadas, '''r y s'''. Trazamos las bisectrices de los ángulos en '''M y N'''. Estas bisectrices se cortan en puntos de la bisectriz '''b''' buscada, porque, por ser intersección de las bisectrices, cada uno de ellos es equidistante de las tres rectas. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 26.gif]] | ||
| + | |||
| + | ===Ángulos de la escuadra y el cartabón=== | ||
| + | |||
| + | La escuadra es un triángulo rectángulo isósceles. Sus ángulos interiores son uno de 90º y dos de 45º. | ||
| + | El cartabón es un triángulo rectángulo escaleno. Sus ángulos miden 90º, 60º y 30º. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 27.gif]] | ||
| + | |||
| + | ===Dibujo de ángulos=== | ||
| + | |||
| + | ====Con la escuadra y el cartabón==== | ||
| + | Es muy fácil colocar adecuadamente la escuadra y el cartabón para dibujar ángulos que sean suma o resta de los que forman los instrumentos. En el ejemplo comprobamos cómo se pueden trazar los ángulos de '''105º, 75º y 15º'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 28.gif]] | ||
| + | |||
| + | Para trasladar un ángulo dado <math>\alpha</math> con la escuadra y el cartabón, se dibujan paralelas a cada lado del ángulo <math>\alpha</math> de modo que pasen por el vértice A deseado. Para trazar paralelas a una dirección se coloca uno de los instrumentos con un lado coincidente con la recta dato y se utiliza el otro para apoyarlo. A continuación se desliza el primero hasta el lugar deseado. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 29.gif]] | ||
| + | |||
| + | ====Con regla y compás==== | ||
| + | Ya hemos aprendido a dibujar ángulos rectos al tratar la perpendicularidad. Ahora vamos a ver como se divide un ángulo recto en tres partes iguales. | ||
| + | Esto se llama '''trisección del ángulo recto'''. No hay construcción gráfica para hacer la trisección de ningún otro ángulo. | ||
| + | |||
| + | Una vez construido un ángulo recto, trazamos un arco de radio arbitrario y centro en su vértice que corta a los lados del ángulo en los puntos '''M y N'''. | ||
| + | Dibujamos otro arco de igual radio con centro en '''N'''. El ángulo '''PAN''' mide 60º, pues los tres puntos definen un triángulo equilátero. Lo que indica que el ángulo '''MAP''' es su complementario y mide '''30º'''. | ||
| + | Si dibujamos un tercer arco con el mismo radio y centro en '''M''', obtenemos el punto '''Q'''. Comprobamos que '''PAQ y QAN''' son ángulos de 30º. Así está hecha la trisección del ángulo recto. | ||
| + | Vamos a aprovechar esta construcción para dibujar el ángulo de '''45º'''. Si prolongamos los arcos '''AP y AQ''' vemos que se cortan en el punto '''B''' que pertenece a la bisectriz del ángulo de partida. Cuando se haya terminado se medirá con el transportador pa ver si el resultado es exacto. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 30.gif]] | ||
| + | |||
| + | Vamos a dibujar directamente '''60º y 30º''', trazando un triángulo equilátero '''PAN''' y su bisectriz. | ||
| + | También vemos cómo usar la trisección del ángulo recto para dibujar '''60º, 30º, 75º y 15º'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 31.gif]] | ||
| + | |||
| + | ====Con transportador==== | ||
| + | |||
| + | El transportador es un instrumento semicircular graduado que nos permite medir ángulos. En los problemas de geometría plana es fundamental construir los ángulos con regla y compás. Esto se considera parte del problema. | ||
| + | En los problemas de geometría descriptiva se dibujan los ángulos con escuadra y cartabón o con transportador. | ||
| + | |||
| + | ===Ángulo formado por dos rectas=== | ||
| + | |||
| + | Dos rectas '''r y t''' se cortan formando cuatro ángulos iguales dos a dos por opuestos al vértice y suplementarios dos a dos. Por norma cuando se pide el ángulo formado por dos rectas siempre se responde indicando el menor. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 32.gif]] | ||
| + | |||
| + | ===Ángulo formado por una recta r y una circunferencia c=== | ||
| + | |||
| + | Es el ángulo formado por la recta '''r''' y la recta '''t''', tangente a la circunferencia '''c''' en el punto '''M''', intersección de la recta con c. El ángulo es el mismo considerando cualquiera de los dos puntos de intersección '''M y N'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 33.gif]] | ||
| + | |||
| + | ===Ángulo formado por dos circunferencias=== | ||
| + | |||
| + | Es el formado por las tangentes '''t y g''' en uno de los puntos de intersección, '''M o N'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 34.gif]] | ||
| + | |||
| + | Si el ángulo entre dos circunferencias es de '''90º''', las circunferencias se llaman '''ortogonales'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 35.gif]] | ||
| + | |||
| + | ===La circunferencia. Nomenclatura=== | ||
| + | |||
| + | La '''circunferencia c''' con '''centro''' en '''C''' es el lugar geométrico de los puntos del plano que equidistan del punto '''C'''. La distancia es el '''radio r''' de la circunferencia y se dibuja uniendo cualquier punto de ella con su centro '''C'''. | ||
| + | Cuando dos circunferencias tienen el mismo centro se llaman [[Circunferencias concéntricas|concéntricas]]. | ||
| + | Dos circunferencias pueden ser '''exteriores, secantes o tangentes'''. En el primer caso no tienen ningún punto común, en el segundo se cortan en dos puntos y en el tercero en un punto que se considera un punto doble. | ||
| + | Con respecto a una circunferencia '''c''', con centro en '''C''', una recta puede ser '''exterior''', como '''e, secante''' como '''s''' y '''tangente''' como '''t'''. | ||
| + | |||
| + | La recta '''t''' es tangente en el '''punto de tangencia T''' y el radio '''CT''' será perpendicular a '''t'''. | ||
| + | Dos puntos '''M y N''' de la circunferencia definen sobre ella dos '''arcos, MHN y MTN'''. | ||
| + | '''M y N''' también definen un segmento rectilíneo '''MN''' interior a la circunferencia, que se llama '''cuerda'''. El radio '''CN''' que pasa por el punto medio '''F''' de una cuerda es perpendicular a ella y define el segmento '''FH''' que se llama '''flecha''' de una cuerda. | ||
| + | Cuando una cuerda pasa por C se llama '''diámetro''' de la circunferencia, como '''DE'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 36.gif]] | ||
| + | |||
| + | ====El círculo. Nomenclatura==== | ||
| + | |||
| + | El '''círculo''' es la parte de plano interior a una circunferencia. El círculo es una superficie y la circunferencia es su perímetro. | ||
| + | En un círculo, una cuerda y uno de sus arcos definen un '''segmento circular'''. | ||
| + | Dos radios y un arco definido por sus extremos limitan un '''sector circular'''. | ||
| + | Dos cuerdas paralelas definen un segmento '''circular de dos bases'''. | ||
| + | Dos circunferencias concéntricas definen una '''corona circular''' que es la diferencia de superficies de los dos círculos. | ||
| + | Dos radios definen un '''trapecio circular''' sobre una corona circular. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 37.gif]] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión de 11:35 29 jul 2013
Definición
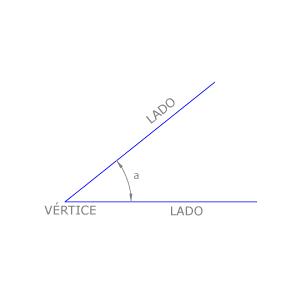
Un ángulo 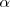 es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo.
es la parte del plano limitada por dos semirrectas que parten del mismo punto, que es el vértice del ángulo. Las semirrectas que lo limitan son los lados del ángulo.
Nomenclatura de los ángulos
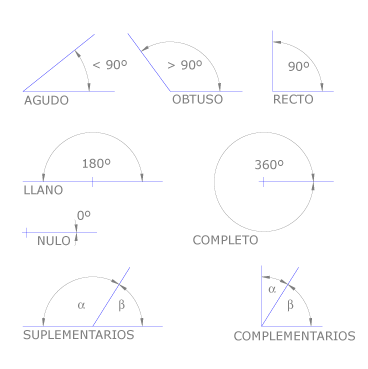
Cuando un ángulo es menor de 90º se llama agudo, si es mayor de 90º se llama obtuso y si mide 90º se llama recto. El ángulo llano o extendido mide 180º, el ángulo completo 360º y el ángulo nulo 0º. Dos ángulos se llaman suplementarios si suman 180º y complementarios si suman 90º.
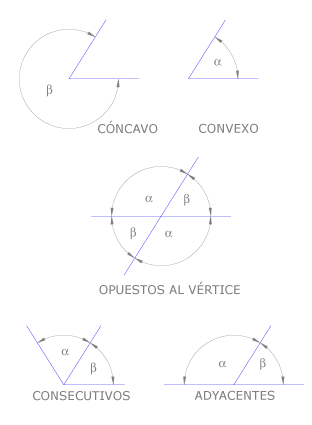
Un ángulo cóncavo mide más de 180º grados. Si se prolonga el lado de un ángulo cóncavo la prolongación divide al ángulo. Un ángulo convexo mide menos de 180º. Aunque se prolonguen sus lados las prolongaciones no dividen el ángulo. Cuando dos rectas se cortan forman cuatro ángulos iguales dos a dos y suplementarios dos a dos. Los que son iguales son opuestos al vértice. Dos ángulos son consecutivos cuando tienen un lado común. Dos ángulos son adyacentes cuando son consecutivos y suplementarios.
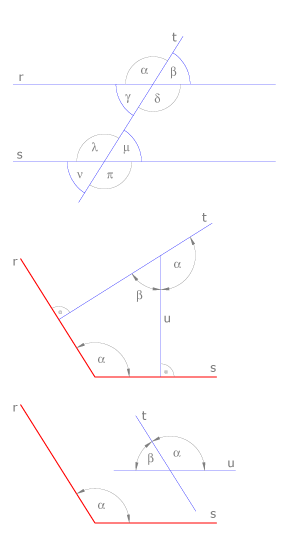
Cuando una recta corta a dos rectas paralelas se forman ángulos que tienen las siguientes características:
Todos tienen un lado común y otro lado en rectas paralelas entre sí.
Hay ángulos que son iguales por ser opuestos al vértice, como 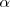 y
y 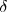 ; otros ángulos iguales se llaman alternos internos, como
; otros ángulos iguales se llaman alternos internos, como 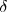 y
y 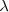 o alternos externos, como
o alternos externos, como 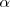 y
y  .
.
Propiedad relativa a los ángulos
Si se trazan dos rectas perpendiculares a los lados de un ángulo, éstas forman un ángulo igual al dado y otro suplementario. Si se trazan dos rectas paralelas a los lados de un ángulo éstas forman un ángulo igual al dado y otro suplementario.
Traslado de un ángulo
Si queremos dibujar un ángulo igual a uno dado con vértice en un punto dado A, dibujamos un arco de radio arbitrario con centro en el vértice del ángulo dado y otro arco igual con centro en A. Medimos con el compás el arco limitado por los lados del ángulo dado y llevamos tal medida con el compás sobre el arco de centro en A.
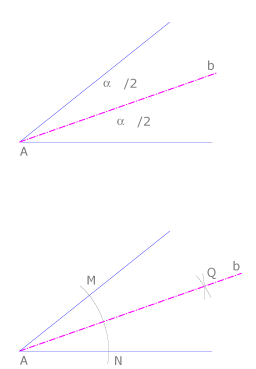
Bisectriz de un ángulo
Es la recta que divide un ángulo en dos partes iguales. La propiedad de cada uno de los puntos de una bisectriz es que equidista de los lados del ángulo. Para trazar una bisectriz se dibuja un arco de radio arbitrario con centro en el vértice. Este arco corta a los lados en los puntos M y N. La bisectriz b es la mediatriz de la cuerda MN.
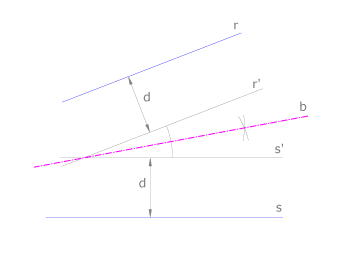
Bisectriz de dos rectas que se cortan fuera del dibujo. Vamos a resolver este problema por dos métodos:
1. Dibujamos dos rectas r’ y s’ paralelas a las dadas, r y s, de modo que la distancia d entre los dos pares de paralelas sea la misma.
La bisectriz b buscada es la bisectriz de r’ y s’.
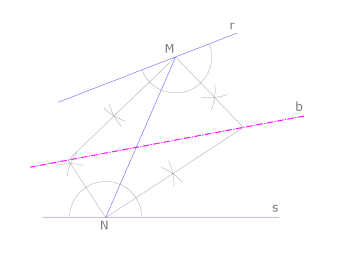
2. Dibujamos un segmento arbitrario MN que tenga un extremo en cada una de las rectas dadas, r y s. Trazamos las bisectrices de los ángulos en M y N. Estas bisectrices se cortan en puntos de la bisectriz b buscada, porque, por ser intersección de las bisectrices, cada uno de ellos es equidistante de las tres rectas.
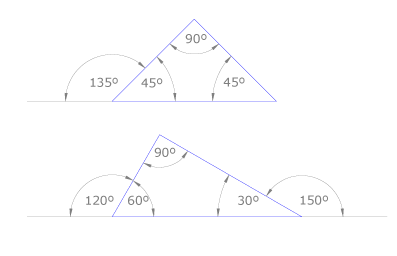
Ángulos de la escuadra y el cartabón
La escuadra es un triángulo rectángulo isósceles. Sus ángulos interiores son uno de 90º y dos de 45º. El cartabón es un triángulo rectángulo escaleno. Sus ángulos miden 90º, 60º y 30º.
Dibujo de ángulos
Con la escuadra y el cartabón
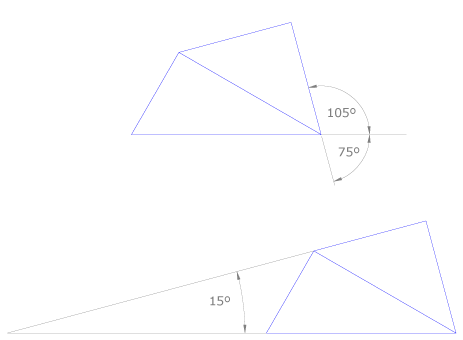
Es muy fácil colocar adecuadamente la escuadra y el cartabón para dibujar ángulos que sean suma o resta de los que forman los instrumentos. En el ejemplo comprobamos cómo se pueden trazar los ángulos de 105º, 75º y 15º.
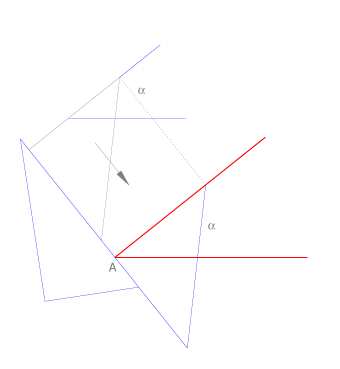
Para trasladar un ángulo dado 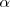 con la escuadra y el cartabón, se dibujan paralelas a cada lado del ángulo
con la escuadra y el cartabón, se dibujan paralelas a cada lado del ángulo 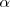 de modo que pasen por el vértice A deseado. Para trazar paralelas a una dirección se coloca uno de los instrumentos con un lado coincidente con la recta dato y se utiliza el otro para apoyarlo. A continuación se desliza el primero hasta el lugar deseado.
de modo que pasen por el vértice A deseado. Para trazar paralelas a una dirección se coloca uno de los instrumentos con un lado coincidente con la recta dato y se utiliza el otro para apoyarlo. A continuación se desliza el primero hasta el lugar deseado.
Con regla y compás
Ya hemos aprendido a dibujar ángulos rectos al tratar la perpendicularidad. Ahora vamos a ver como se divide un ángulo recto en tres partes iguales. Esto se llama trisección del ángulo recto. No hay construcción gráfica para hacer la trisección de ningún otro ángulo.
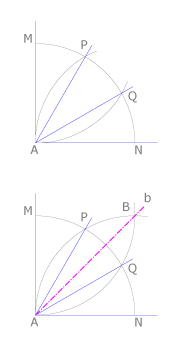
Una vez construido un ángulo recto, trazamos un arco de radio arbitrario y centro en su vértice que corta a los lados del ángulo en los puntos M y N. Dibujamos otro arco de igual radio con centro en N. El ángulo PAN mide 60º, pues los tres puntos definen un triángulo equilátero. Lo que indica que el ángulo MAP es su complementario y mide 30º. Si dibujamos un tercer arco con el mismo radio y centro en M, obtenemos el punto Q. Comprobamos que PAQ y QAN son ángulos de 30º. Así está hecha la trisección del ángulo recto. Vamos a aprovechar esta construcción para dibujar el ángulo de 45º. Si prolongamos los arcos AP y AQ vemos que se cortan en el punto B que pertenece a la bisectriz del ángulo de partida. Cuando se haya terminado se medirá con el transportador pa ver si el resultado es exacto.
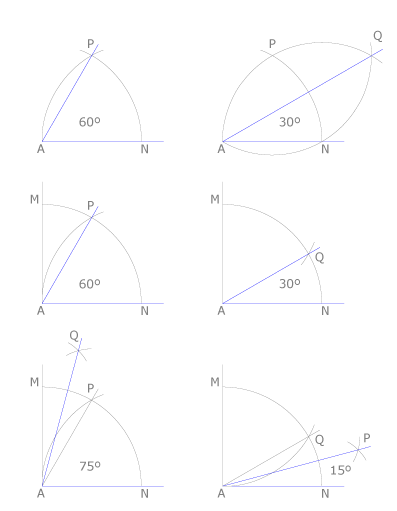
Vamos a dibujar directamente 60º y 30º, trazando un triángulo equilátero PAN y su bisectriz. También vemos cómo usar la trisección del ángulo recto para dibujar 60º, 30º, 75º y 15º.
Con transportador
El transportador es un instrumento semicircular graduado que nos permite medir ángulos. En los problemas de geometría plana es fundamental construir los ángulos con regla y compás. Esto se considera parte del problema. En los problemas de geometría descriptiva se dibujan los ángulos con escuadra y cartabón o con transportador.
Ángulo formado por dos rectas
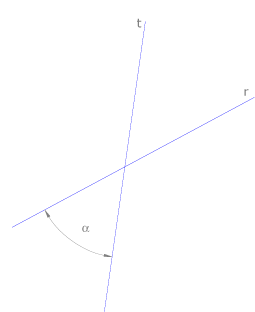
Dos rectas r y t se cortan formando cuatro ángulos iguales dos a dos por opuestos al vértice y suplementarios dos a dos. Por norma cuando se pide el ángulo formado por dos rectas siempre se responde indicando el menor.
Ángulo formado por una recta r y una circunferencia c
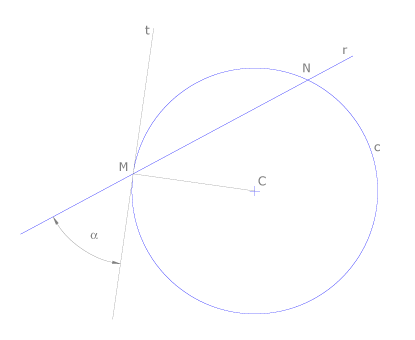
Es el ángulo formado por la recta r y la recta t, tangente a la circunferencia c en el punto M, intersección de la recta con c. El ángulo es el mismo considerando cualquiera de los dos puntos de intersección M y N.
Ángulo formado por dos circunferencias
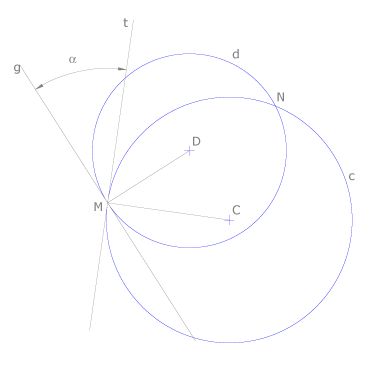
Es el formado por las tangentes t y g en uno de los puntos de intersección, M o N.
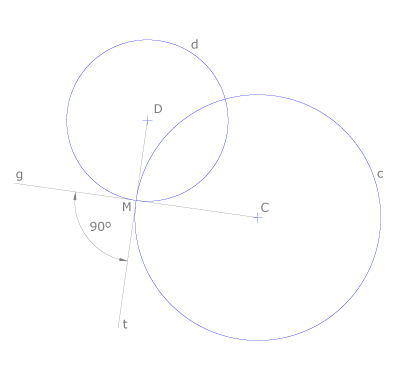
Si el ángulo entre dos circunferencias es de 90º, las circunferencias se llaman ortogonales.
La circunferencia. Nomenclatura
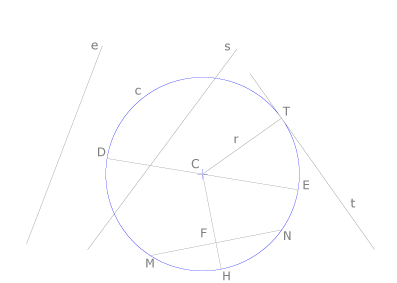
La circunferencia c con centro en C es el lugar geométrico de los puntos del plano que equidistan del punto C. La distancia es el radio r de la circunferencia y se dibuja uniendo cualquier punto de ella con su centro C. Cuando dos circunferencias tienen el mismo centro se llaman concéntricas. Dos circunferencias pueden ser exteriores, secantes o tangentes. En el primer caso no tienen ningún punto común, en el segundo se cortan en dos puntos y en el tercero en un punto que se considera un punto doble. Con respecto a una circunferencia c, con centro en C, una recta puede ser exterior, como e, secante como s y tangente como t.
La recta t es tangente en el punto de tangencia T y el radio CT será perpendicular a t. Dos puntos M y N de la circunferencia definen sobre ella dos arcos, MHN y MTN. M y N también definen un segmento rectilíneo MN interior a la circunferencia, que se llama cuerda. El radio CN que pasa por el punto medio F de una cuerda es perpendicular a ella y define el segmento FH que se llama flecha de una cuerda. Cuando una cuerda pasa por C se llama diámetro de la circunferencia, como DE.
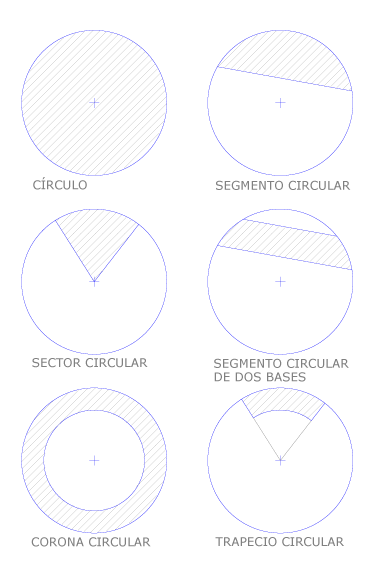
El círculo. Nomenclatura
El círculo es la parte de plano interior a una circunferencia. El círculo es una superficie y la circunferencia es su perímetro. En un círculo, una cuerda y uno de sus arcos definen un segmento circular. Dos radios y un arco definido por sus extremos limitan un sector circular. Dos cuerdas paralelas definen un segmento circular de dos bases. Dos circunferencias concéntricas definen una corona circular que es la diferencia de superficies de los dos círculos. Dos radios definen un trapecio circular sobre una corona circular.
Tweet