Concavidad y convexidad
De Wikillerato
(Diferencias entre revisiones)
| Línea 76: | Línea 76: | ||
<br/> | <br/> | ||
| + | |||
| + | ==Punto de inflexión== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Un punto de inflexion es un punto donde la función pasa de ser concava a convexa o | ||
| + | viceversa. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | es un punto de inflexión de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | , entonces | ||
| + | <math> | ||
| + | \mathrm{f}^{\prime \prime} \left( \, x_0 \, \right) \, = \, 0 | ||
| + | </math>. | ||
| + | Pero lo reciproco no es cierto: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \mathrm{f}^{\prime \prime} \left( \, x_0 \, \right) \, = \, 0 | ||
| + | </math> | ||
| + | no implica que | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | sea un punto de inflexión de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 03:23 15 ene 2007
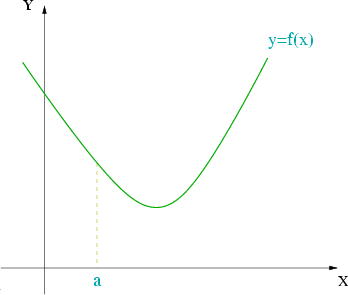
Convexidad
Si la derivada segunda de
 en
en
 es positiva, entonces
es positiva, entonces
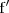 es creciente en
es creciente en
 y
y
 es convexa en
es convexa en
 .
.
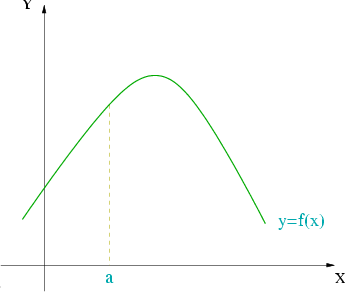
Concava
Si la derivada segunda de
 en
en
 es negativa, entonces
es negativa, entonces
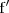 es decreciente en
es decreciente en
 y
y
 es concava en
es concava en
 .
.
Punto de inflexión
Un punto de inflexion es un punto donde la función pasa de ser concava a convexa o viceversa.
Si
 es un punto de inflexión de
es un punto de inflexión de
 , entonces
, entonces
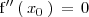 .
Pero lo reciproco no es cierto:
.
Pero lo reciproco no es cierto:
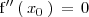 no implica que
no implica que
 sea un punto de inflexión de
sea un punto de inflexión de
 .
.