Navegación
Lógica proposicional
De Wikillerato
| Línea 30: | Línea 30: | ||
Ejemplos de simbolización de oraciones, del lenguaje natural al lenguaje formal: | Ejemplos de simbolización de oraciones, del lenguaje natural al lenguaje formal: | ||
| - | 1. La conjunción: [ p | + | 1. La conjunción: <math>[ p \land q ]</math> “Juan juega y Pedro estudia”. |
| - | 2. La disyunción: [ p | + | 2. La disyunción: <math>[ p \lor q ]</math> “Llueve o nieva”. |
| - | 3. El condicional: [ p | + | 3. El condicional: <math>[ p \to q ]</math> “Si estudias entonces aprendes”. |
| - | 4. El bicondicional: [ p | + | 4. El bicondicional: <math>[ p \leftrightarrow q ]</math> “Si y sólo si tienes dieciocho años puedes votar”. |
| - | 5. La disyunción exclusiva: [ p | + | 5. La disyunción exclusiva: <math>[ p \lor q ]</math> “O te quedas o te vas”. |
| - | 6. La negación: [ | + | 6. La negación: <math>[ \bar{p} ]</math> “Manolo no juega limpio”. |
A veces el negador puede afectar a más de una variable o a la conjunción, o disyunción de ambas: | A veces el negador puede afectar a más de una variable o a la conjunción, o disyunción de ambas: | ||
| - | [ ] “Es falso que estudies o trabajes”. | + | <math>[\bar{p \lor q} ]</math> “Es falso que estudies o trabajes”. |
Revisión de 15:39 12 mar 2007
Una de las razones que motivó la aparición de la lógica matemática, fue evitar la ambigüedad del lenguaje natural y transformar el pensamiento en un cálculo, según el modo de operar de las matemáticas. Simplificar o simbolizar las oraciones o juicios para poder operar con ellas, así surge el
Lenguaje formal
Consiste en abreviar o simbolizar las oraciones o juicios, que en la lógica matemática se llaman proposiciones. Estas proposiciones se reducen en el lenguaje formal a una sola letra, que llamamos variable, y la simbolizamos con las letras minúsculas del alfabeto que van de la “p” hasta el final del abecedario.
Si digo por ejemplo:”Antonio ama a Piedad”, esta proposición queda simbolizada en el lenguaje formal mediante la variable “p” o “q”, o “r”, o “s”.
Además de estas variables, la lógica proposicional utiliza otros símbolos, llamados constantes, cuyo significado siempre es el mismo ya que modifican o unen a las variables. Estos símbolos constantes, se llaman funtores, juntores, conectivas u operadores lógicos.
Cuando el funtor afecta a una sola variable, se llama monádico, como por ejemplo el negador ( 
) que se lee en el lenguaje natural “no”, y se sitúa encima de la letra variable,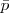 
, “no p”. Cuando afectan a más de una variable, son poliádicos.
Los funtores más importantes son:
![[\land ]](/images/math/math-baf992ff0c986159b9c5ef70e7e29e55.png "[\land ]")
Conjuntor , “ y “ en el lenguaje natural.
![[\lor ]](/images/math/math-bd8c0a940b89c20533d0b080b5224de6.png "[\lor ]")
Disyuntor , “ o “.
![[\to ]](/images/math/math-5c949e1f45fa0ca747c04cdf0101940c.png "[\to ]")
Condicional, “ si…, entonces”.
![[\leftrightarrow ]](/images/math/math-bb19fe548f207855642cd1fd75bb3aca.png "[\leftrightarrow ]")
Bicondiconal, “ si y sólo si…, entonces”.
Disyunción exclusiva, “o…o”, una proposición excluye a la otra.
El negador además de ser un funtor monádico, es decir que afecta a una variable, puede ser poliádico, cuando afecta a más de una variable o a una expresión entera.
Hay que tener siempre en cuenta, que las variables simbolizan oraciones enteras y no sólo palabras o nombres:
Ejemplos de simbolización de oraciones, del lenguaje natural al lenguaje formal:
1. La conjunción: ![[ p \land q ]](/images/math/math-2cd2ecd36dbd562c6b70fedbceb358ff.png "[ p \land q ]")
“Juan juega y Pedro estudia”.
2. La disyunción: ![[ p \lor q ]](/images/math/math-c919ef3ec2077fe7abd6e9a3bd7099cb.png "[ p \lor q ]")
“Llueve o nieva”.
3. El condicional: ![[ p \to q ]](/images/math/math-202695fcd5d9899b7d9c76f19b3ca0a2.png "[ p \to q ]")
“Si estudias entonces aprendes”.
4. El bicondicional: ![[ p \leftrightarrow q ]](/images/math/math-53c3106d4bf4a887b9e0b5b1caf002c2.png "[ p \leftrightarrow q ]")
“Si y sólo si tienes dieciocho años puedes votar”.
5. La disyunción exclusiva: ![[ p \lor q ]](/images/math/math-e4001a75c1dfe933123ed05cfc280cdd.png "[ p \lor q ]")
“O te quedas o te vas”.
6. La negación: ![[ \bar{p} ]](/images/math/math-4e0de1fd168b7d9b5d2909ae35ffdec9.png "[ \bar{p} ]")
“Manolo no juega limpio”.
A veces el negador puede afectar a más de una variable o a la conjunción, o disyunción de ambas:
![[\bar{p \lor q} ]](/images/math/math-68a219fa52c7fef29a036b1776621164.png "[\bar{p \lor q} ]")
“Es falso que estudies o trabajes”.
