Navegación
Lógica de clases
De Wikillerato
(→Elementos de una clase) |
(→Elementos de una clase) |
||
| Línea 7: | Línea 7: | ||
==Elementos de una clase== | ==Elementos de una clase== | ||
| - | Cada uno de los objetos integrantes de una clase, es un elemento o miembro de la clase. La relación existente entre un elemento y la clase de la que es miembro, se llama relación de pertenencia, el elemento pertenece a la clase, se simboliza: [<math> \in</math> ]; este símbolo deriva de la palabra griega estí, que significa es. Por ejemplo | + | Cada uno de los objetos integrantes de una clase, es un elemento o miembro de la clase. La relación existente entre un elemento y la clase de la que es miembro, se llama relación de pertenencia, el elemento pertenece a la clase, se simboliza: [<math> \in</math> ]; este símbolo deriva de la palabra griega estí, que significa es. Por ejemplo Madrid pertenece a las capitales europeas. <math>Madrid \in C</math>. |
| - | En general <math>x \in C</math>, quiere decir que <math> x</math> es un elemento de <math>C</math>. Cuando quiero expresar que un elemento no pertenece a una clase, utilizo el símbolo: <math>\notin</math> . Por ejemplo México<math> \notin C</math>, quiere decir que México no pertenece a las capitales europeas. | + | En general <math>x \in C</math>, quiere decir que <math> x</math> es un elemento de <math>C</math>. Cuando quiero expresar que un elemento no pertenece a una clase, utilizo el símbolo: <math>\notin</math> . Por ejemplo México <math> \notin C</math>, quiere decir que México no pertenece a las capitales europeas. |
Las clases se pueden definir por '''extensión y comprensión'''. Por extensión enumerando sus elementos; por comprensión expresando sus propiedades comunes. | Las clases se pueden definir por '''extensión y comprensión'''. Por extensión enumerando sus elementos; por comprensión expresando sus propiedades comunes. | ||
La comprensión expresa su definición en términos de idea o concepto, es decir el significado de la clase o del concepto. La extensión hace referencia a sus elementos o bien de forma total: <math>\forall x</math> o bien de forma parcial: <math>\exists x</math> . | La comprensión expresa su definición en términos de idea o concepto, es decir el significado de la clase o del concepto. La extensión hace referencia a sus elementos o bien de forma total: <math>\forall x</math> o bien de forma parcial: <math>\exists x</math> . | ||
Revisión de 08:53 2 abr 2007
Clases
Se entiende por clase una pluralidad o conjunto de individuos que tienen una misma propiedad o propiedades. Según el diagrama de la introducción a la lógica, en la lógica proposicional, hemos estudiado las oraciones o juicios, las proposiciones y los razonamientos. En la lógica de clases, nos ocupamos de los conceptos que designan un grupo de objetos con las mismas propiedades o características. Estos grupos de objetos, son las clases.
En el lenguaje formal las clases se representan con letras mayúsculas empezando por la 
.
Elementos de una clase
Cada uno de los objetos integrantes de una clase, es un elemento o miembro de la clase. La relación existente entre un elemento y la clase de la que es miembro, se llama relación de pertenencia, el elemento pertenece a la clase, se simboliza: [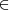
]; este símbolo deriva de la palabra griega estí, que significa es. Por ejemplo Madrid pertenece a las capitales europeas. 
.
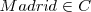En general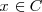 
, quiere decir que 
es un elemento de 
. Cuando quiero expresar que un elemento no pertenece a una clase, utilizo el símbolo: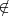 
. Por ejemplo México 
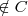, quiere decir que México no pertenece a las capitales europeas.
Las clases se pueden definir por extensión y comprensión. Por extensión enumerando sus elementos; por comprensión expresando sus propiedades comunes.
La comprensión expresa su definición en términos de idea o concepto, es decir el significado de la clase o del concepto. La extensión hace referencia a sus elementos o bien de forma total: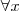 
o bien de forma parcial: 
.
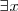