Experiencia para obtener la Ley de Hooke
De Wikillerato
| Línea 45: | Línea 45: | ||
Si una vez alcanzado el equilibrio, es decir cuando | Si una vez alcanzado el equilibrio, es decir cuando | ||
| - | + | <math> \vec F + m \vec g = 0<\math> | |
tiramos de <math>m</math>, produciendo en el resorte un alargamiento suplementario <math>A</math>, con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio <math>O</math>, repitiéndose periódicamente su posición con respecto a <math>O</math>. Un movimiento de estas características es denominado movimiento oscilatorio armónico o movimiento armónico simple. | tiramos de <math>m</math>, produciendo en el resorte un alargamiento suplementario <math>A</math>, con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio <math>O</math>, repitiéndose periódicamente su posición con respecto a <math>O</math>. Un movimiento de estas características es denominado movimiento oscilatorio armónico o movimiento armónico simple. | ||
El movimiento se inicia porque al deformar el resorte (estirarlo o comprimirlo) le aportamos una energía que el resorte desarrolla al dejarlo en libertad. Esta energía será una energía potencial, puesto que la definición que hemos dado de ésta siempre ha sido la capacidad del sistema para desarrollar un trabajo. Veamos cuál es en el sistema que estudiamos. | El movimiento se inicia porque al deformar el resorte (estirarlo o comprimirlo) le aportamos una energía que el resorte desarrolla al dejarlo en libertad. Esta energía será una energía potencial, puesto que la definición que hemos dado de ésta siempre ha sido la capacidad del sistema para desarrollar un trabajo. Veamos cuál es en el sistema que estudiamos. | ||
Revisión de 09:47 17 sep 2007
Medida experimental de la Constante de elasticidad de un resorte. Calibrado de un dinamómetro.
Material: Pie, varilla, nuez y pinza (pinza con nuez), resorte, pesas, regla, papel mm.
Objetivo: Se trata de obtener una ley demostrada empíricamente, mediante la relación que puede establecerse entre dos parámetros, fuerza y deformación de los cuerpos elásticos, hallando una ecuación en la que se relacionan de modo directamente proporcional. Aprendizaje del dibujo de gráficas. Dibujar la recta de regresión que nos permita calcular una constante de proporcionalidad.
Método:
En primer lugar suspenderemos una masa 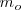 de modo que esteremos seguros de que el resorte se encuentre perfectamente estirado y no queden espiras yuxtapuestas, mediremos la marca que, sobre la regla, marque el extremo inferior del resorte.
A esta medida la llamaremos
de modo que esteremos seguros de que el resorte se encuentre perfectamente estirado y no queden espiras yuxtapuestas, mediremos la marca que, sobre la regla, marque el extremo inferior del resorte.
A esta medida la llamaremos 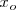 . Obtendremos pues dos medidas relacionadas entre sí:
. Obtendremos pues dos medidas relacionadas entre sí:
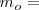 [introducir datos] y
[introducir datos] y 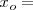 [introducir datos]
[introducir datos]
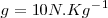
A continuación, se irán suspendiendo del extremo inferior del resorte diferentes masas y se irá construyendo la tabla de valores siguiente
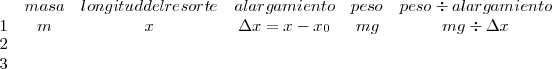
Construcción de gráficas
Sobre una hoja de papel mm se representará 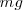 en ordenadas y
en ordenadas y 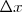 en abcisas.
en abcisas.
Se obtendrán una serie de puntos que se encuentren más o menos alineados.
Se trazará la línea que contenga el mayor numero de esos puntos y, en el caso de que no contenga a todos, que deje igual número de puntos por encima que por debajo. A esta recta se le llama recta de regresión. Su pendiente, nos indica la razón de proporcionalidad entre fuerza y alargamiento, que es la constante de proporcionalidad del resorte, 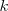 .
.
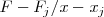 , es decir
, es decir 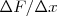 este cociente, y, por lo tanto
este cociente, y, por lo tanto 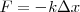
Aplicaciones:
Calibrado de dinamómetros que nos permitirán medir fuerzas. Amortiguadores de automóviles. Resortes de los asientos. Camas elásticas. Elasticidad de la madera en las pértigas y tablones de trampolines. Elasticidad de los materiales con que se fabrican las pelotas de los diferentes juegos deportivos. Elasticidad de las vigas y cables de acero en los puentes.
Si una vez alcanzado el equilibrio, es decir cuando
[Unparseable or potentially dangerous latex formula. Error 3 ], produciendo en el resorte un alargamiento suplementario  , con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio
, con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio 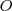 , repitiéndose periódicamente su posición con respecto a
, repitiéndose periódicamente su posición con respecto a 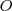 . Un movimiento de estas características es denominado movimiento oscilatorio armónico o movimiento armónico simple.
. Un movimiento de estas características es denominado movimiento oscilatorio armónico o movimiento armónico simple.
El movimiento se inicia porque al deformar el resorte (estirarlo o comprimirlo) le aportamos una energía que el resorte desarrolla al dejarlo en libertad. Esta energía será una energía potencial, puesto que la definición que hemos dado de ésta siempre ha sido la capacidad del sistema para desarrollar un trabajo. Veamos cuál es en el sistema que estudiamos.
Tweet


