Navegación
Energía de un oscilador armónico
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | ==Introducción== | ||
| + | |||
Cuando deformamos el resorte una longitud <math>A</math> con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será <math>F = - k A</math>. Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero. | Cuando deformamos el resorte una longitud <math>A</math> con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será <math>F = - k A</math>. Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero. | ||
| Línea 36: | Línea 38: | ||
Es decir, la aceleración es proporcional a la distancia a la posición de equilibrio pero con sentido opuesto. | Es decir, la aceleración es proporcional a la distancia a la posición de equilibrio pero con sentido opuesto. | ||
| + | |||
| + | ==Parámetros del movimiento oscilatorio== | ||
| + | |||
| + | ==Ecuación del movimiento oscilatorio== | ||
| + | |||
| + | ==Velocidad y aceleración del m.o.a== | ||
| + | |||
| + | ==Relación entre los parámetros== | ||
[[Categoría:Física|Oscilador armónico]] | [[Categoría:Física|Oscilador armónico]] | ||
Revisión de 11:23 17 sep 2007
Tabla de contenidos |
Introducción
Cuando deformamos el resorte una longitud 
con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será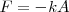 
. Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero.
La energía que es capaz de desarrollar el resorte es:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Donde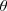 
es el ángulo formado por 
e 
, que en nuestro caso, dado que la y la deformación tienen siempre sentidos opuestos, el ángulo es 
, y como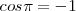 
. Como por otra parte el valor máximo de 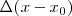es , la ecuación de la energía del oscilador será:
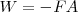
La fuerza es variable, y varía entre los valores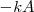 
y 
. Esta variación es lineal y, en consecuencia podremos sustituirla en la ecuación por su valor medio, que será la semisuma de los valores máximo 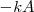y mínimo, .
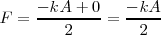
La energía máxima del resorte será:
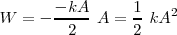
Es decir, la energía sólo depende de la constante de elasticidad del resorte y de la distancia a la posición de equilibrio. Y es, en los extremos, una energía potencial elástica.
Cuando estiramos el resorte una longitud y soltamos, el resorte comienza a moverse, desde una velocidad cero, en los extremos, puesto que pasa de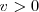 
a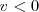 
y viceversa, a un valor máximo cuando el resorte pasa por la posición de equilibrio.
La energía asociada al movimiento es la energía cinética, y será, al pasar por la posición de equilibrio, igual a la energía potencial máxima, tendremos
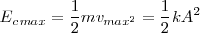
Pero el oscilador, en su movimiento, pasará por una posición 
en la cual llevará una velocidad 
, y la ecuación de la energía del movimiento nos quedará
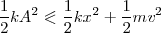
Es decir, la energía total se conserva y es igual, en cada instante, a la suma de la energía potencial y de la energía cinética
En todo caso, no debemos olvidar nunca que siempre ha de cumplirse la segunda ley de Newton
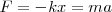
De donde obtenemos que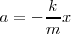 
Es decir, la aceleración es proporcional a la distancia a la posición de equilibrio pero con sentido opuesto.
