Funciones y gráficas
De Wikillerato
(→Definición) |
|||
| Línea 1: | Línea 1: | ||
| - | y= | + | ==Definición== |
| - | + | ||
| - | x- | + | <br/> |
| + | |||
| + | Una '''''función real de variable real''''' es toda correspondencia | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | que asocia a cada elemento | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | de un subconjunto no vacio | ||
| + | <math> | ||
| + | D | ||
| + | </math> | ||
| + | de | ||
| + | <math> | ||
| + | R | ||
| + | </math> | ||
| + | un único número real. La expresamos como: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{f}: D \subset R \longrightarrow R | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | x \longrightarrow y \, = \, \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | es la '''''variable independiente''''' e | ||
| + | <math> | ||
| + | y | ||
| + | </math> | ||
| + | la '''''variable dependiente.''''' | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Al conjunto, | ||
| + | <math> | ||
| + | D | ||
| + | </math> | ||
| + | , de valores que toma la variable independiente | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | se le llama '''''dominio''''' de la función. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Al conjunto de valores que toma la variable dependiente | ||
| + | <math> | ||
| + | y | ||
| + | </math> | ||
| + | se le llama '''''recorrido''''' de la función. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función se define '''''explicitamente''''' si viene dada como | ||
| + | <math> | ||
| + | y \, = \, \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | , es decir, si la variable dependiente, | ||
| + | <math> | ||
| + | y | ||
| + | </math> | ||
| + | , esta despejada. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función se define '''''implícitamente''''' si viene dada en la forma | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | \left( | ||
| + | \, x, \, y \, | ||
| + | \right) | ||
| + | \, = \, 0 | ||
| + | </math> | ||
| + | , esto es, si la función se expone como una expresión algebraica igualada a cero. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La función | ||
| + | <math> | ||
| + | y \, = \, \cos \left( \, x \, \right) | ||
| + | </math> | ||
| + | está expresada en forma explícita. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La función | ||
| + | <math> | ||
| + | \log y \, - \, x \, = \, 0 | ||
| + | </math> | ||
| + | está expresada en forma implícita. | ||
| + | |||
| + | <br/> | ||
==Gráfica== | ==Gráfica== | ||
Revisión de 18:56 29 ene 2008
Tabla de contenidos |
Definición
Una función real de variable real es toda correspondencia
 que asocia a cada elemento
que asocia a cada elemento
 de un subconjunto no vacio
de un subconjunto no vacio
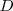 de
de
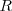 un único número real. La expresamos como:
un único número real. La expresamos como:
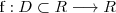
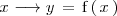
 es la variable independiente e
es la variable independiente e
 la variable dependiente.
la variable dependiente.
Al conjunto,
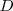 , de valores que toma la variable independiente
, de valores que toma la variable independiente
 se le llama dominio de la función.
se le llama dominio de la función.
Al conjunto de valores que toma la variable dependiente
 se le llama recorrido de la función.
se le llama recorrido de la función.
Una función se define explicitamente si viene dada como
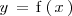 , es decir, si la variable dependiente,
, es decir, si la variable dependiente,
 , esta despejada.
, esta despejada.
Una función se define implícitamente si viene dada en la forma
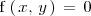 , esto es, si la función se expone como una expresión algebraica igualada a cero.
, esto es, si la función se expone como una expresión algebraica igualada a cero.
Ejemplo
La función
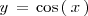 está expresada en forma explícita.
está expresada en forma explícita.
La función
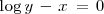 está expresada en forma implícita.
está expresada en forma implícita.
Gráfica
La gráfica de una función
 es el conjunto de puntos del plano definido de la siguiente forma:
es el conjunto de puntos del plano definido de la siguiente forma:
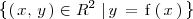
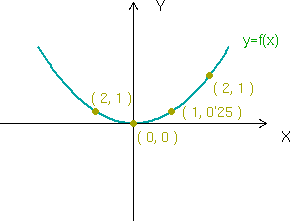
Ejemplo
La figura de abajo muestra la gráfica de la funcion
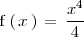 y cuatro puntos de la misma:
y cuatro puntos de la misma: