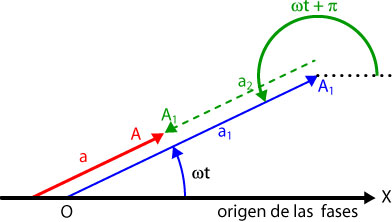
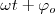Composición de movimientos oscilatorios armónicos
De Wikillerato
(→Composiciones de movimientos oscilatorios perpendiculares. - Figuras de Lissajous) |
(→Composiciones de movimientos oscilatorios perpendiculares. - Figuras de Lissajous) |
||
| Línea 226: | Línea 226: | ||
<math> \frac{y}{x} = - \frac{b}{a} </math> | <math> \frac{y}{x} = - \frac{b}{a} </math> | ||
| + | |||
| + | '''Cuando''' <math>\delta = 0 \ o \ \pi</math> la interferencia de dos movimientos armónicos simples de igual frecuencia producen una polarización rectilínea. | ||
| + | |||
| + | Si las dos movimientos son de igual amplitud y <math> \delta = 0</math> <math> \frac {y}{x} \ = 1</math> | ||
| + | |||
| + | Que es la '''''diagonal de un cuadrado de lado a.''''' | ||
| + | |||
| + | Si <math>a = b</math> y, además, <math>\delta = \pi</math> tenemos <math> \frac {y}{x} \ = -1</math> | ||
| + | |||
| + | Si <math>\delta = \frac {\pi} {2}</math> | ||
| + | |||
| + | <math>x = a sen \omega \ t</math> | ||
| + | |||
| + | <math>y = b sen \left ( \omega \ t + \frac {\pi} {2} \right ) = b \ cos \omega \ t </math> | ||
| + | |||
| + | <math> \frac {x}{a} \ = sen \ \omega \ t </math> | ||
| + | <math> \frac {y}{b} \ = cos \ \omega \ t </math> | ||
| + | |||
| + | Elevando al cuadrado y sumando tenemos | ||
| + | |||
| + | <math> \frac {x^2}{a^2} \ + \frac {y^2}{b^2} \ = 1</math> | ||
| + | |||
| + | que es la ecuación de una ''' elipse.''' | ||
| + | |||
| + | En el caso de que <math>a = b </math>, queda <math>x^2 + y^2 = a^2 </math> que es la ecuación de una '''circunferencia'''. | ||
| + | |||
| + | El sentido de giro del movimiento al describir la elipse nos viene dado por el valor de la pendiente de la tangente en <math>x = a</math>, que es la velocidad. | ||
| + | |||
| + | En <math>x = a</math> tenemos <math>a = a \ sen \omega \ t </math>, con lo cual <math>sen \omega \ t = 1</math> | ||
| + | |||
| + | Derivando y con respecto <math>a \ t</math> | ||
Revisión de 08:53 27 mar 2008
Tabla de contenidos
|
Figuras de Lissajous
La composición de movimientos oscilatorios armónicos - que siempre se tratará de pequeñas oscilaciones pues de lo contrario el movimiento será oscilatorio pero no armónico – se realiza como vimos en la composición rectilíneos. Es decir, la elongación del movimiento resultante, será la suma vectorial de las pequeñas elongaciones de los movimientos que lo constituyen.
Si dos movimientos oscilatorios son capaces de enviar energía sobre un punto P, provocando sendos desplazamientos 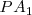 y
y 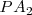 , y esta acción la realizan simultáneamente, el desplazamiento efectuado por
, y esta acción la realizan simultáneamente, el desplazamiento efectuado por 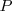 será la suma geométrica de los desplazamientos
será la suma geométrica de los desplazamientos 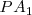 y
y 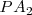 .
.
El caso más frecuente es el de movimientos oscilatorios que tienen lugar sobre la misma recta, es decir, que las elongaciones son paralelas. En este caso, la composición geométrica de los vectores se limita a una suma algebraica de las elongaciones, considerando la recta soporte como un eje de ordenadas.
Construcción de Fresnel
Agustín Fresnel (1788-1827), físico francés.
Muy retrasado en sus estudios durante la infancia – no aprendió a leer hasta los ocho años- que vivió en plena revolución francesa, sin embargo, con dieciséis se graduó con honores en el Escuela Politécnica, que es el centro más prestigioso de Francia. Trabajó en la Vendée, región conocida por su apoyo al antiguo régimen. Apoyó a los Borbones contra Napoleón, por lo que en 1814, y hasta Waterloo, fue destituido de su cargo. Con la restauración del régimen absolutista de los dos últimos Borbones, fue nombrado para un puesto de ingeniero en París.
Como se ve en otro lugar, Fresnel explica completamente los fenómenos de interferencias y de difracción. En 1815 publicó su primer libro en el que explicaba la teoría ondulatoria de la luz, haciendo frente a los que mantenían la teoría corpuscular enunciada por Newton. Pese a su juventud, en 1823 fue elegido miembro de la Academia de Ciencias de Francia y en 1827 fue elegido miembro de la Royal Society de Londres. En pleno romanticismo, murió de tuberculosis al año siguiente con 39 años.
La comprensión de la composición de movimientos vibratorios paralelos queda largamente facilitada por un método gráfico ideado por Fresnel.
Vector giratorio convencional
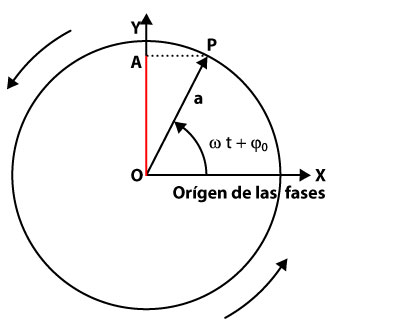
Recordemos la analogía entre el movimiento oscilatorio y la proyección de un radiovector sobre uno de los diámetros de la circunferencia que describe.
Si estudiamos la variación de 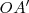 , proyección de
, proyección de 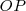 sobre el eje de ordenadas,
sobre el eje de ordenadas, 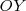 , la medida de esa proyección viene dada por
, la medida de esa proyección viene dada por
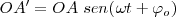
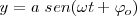
que es la ecuación horaria de un movimiento oscilatorio armónico, donde  es la velocidad angular del movimiento de
es la velocidad angular del movimiento de  , la pulsación del segmento
, la pulsación del segmento 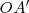 ,
, 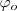 es la constante de fase, o ángulo que ha barrido ya
es la constante de fase, o ángulo que ha barrido ya 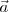 en el instante en que comenzamos a contar el tiempo.
en el instante en que comenzamos a contar el tiempo. 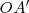 es la elongación
es la elongación 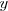 siendo ala elongación máxima o amplitud.
siendo ala elongación máxima o amplitud.
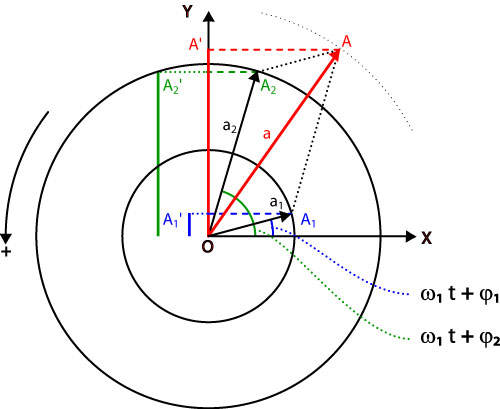
Construcción de Fresnel
Si componemos las dos vibraciones representadas por:
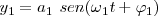
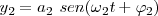
En un instante dado, la representación de sendos radiovectores son  y
y 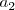 respectivamente.
respectivamente.
Sus proyecciones sobre el eje 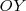 son
son 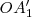 y
y 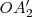 .
.
Por otra parte se conoce la propiedad de la geometría de vectores que dice que la proyección de la suma geométrica de varios vectores sobre un eje es igual a la suma algebraica de las proyecciones de cada uno de los sumandos sobre el mismo eje.
Por lo tanto, la suma
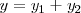
está representada por
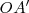 =
= 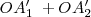 obteniendo la 'Regla de Fresnel',
obteniendo la 'Regla de Fresnel',
“En un instante dado, el vector 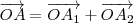 representa el movimiento resultante de la composición de movimientos cuyas elongaciones sean
representa el movimiento resultante de la composición de movimientos cuyas elongaciones sean
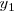

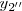
Este método, nos permite obtener la elongación del movimiento resultante dos (o varios) movimientos de elongaciones paralelas, ahorrándonos cálculos trigonómetricos laboriosos por construcciones geométricas.
No debemos olvidar que no se ha dicho aún nada sobre los valores que pueden tomar las pulsaciones 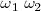 , las cuales pueden ser iguales o diferentes.
, las cuales pueden ser iguales o diferentes.
Si 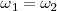 , las frecuencias
, las frecuencias 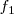 y
y 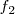 de los movimientos componentes son iguales, el movimiento resultante viene representado por la diagonal
de los movimientos componentes son iguales, el movimiento resultante viene representado por la diagonal 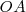 del paralelogramo
del paralelogramo 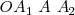 que es indeformable. Este paralelogramo gira alrededor de
que es indeformable. Este paralelogramo gira alrededor de 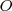 con una velocidad angular
con una velocidad angular 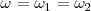 .
.
Este método, nos permite obtener la elongación del movimiento resultante dos (o varios) movimientos de elongaciones paralelas, ahorrándonos cálculos trigonómetricos laboriosos por construcciones geométricas.
No debemos olvidar que no se ha dicho aún nada sobre los valores que pueden tomar las pulsaciones 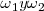 , las cuales pueden ser iguales o diferentes.
, las cuales pueden ser iguales o diferentes.
Si 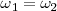 , las frecuencias
, las frecuencias 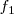 y
y 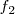 de los movimientos componentes son iguales, el movimiento resultante viene representado por la diagonal
de los movimientos componentes son iguales, el movimiento resultante viene representado por la diagonal 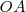 del paralelogramo
del paralelogramo 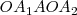 que es indeformable. Este paralelogramo gira alrededor de
que es indeformable. Este paralelogramo gira alrededor de 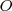 con una velocidad angular
con una velocidad angular 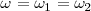 .
.
De un modo general, al igual que se definió la resultante de n vectores al vector que une el origen del primer sumando con el extremo del último, habiéndolos situado uno a continuación del otro, construyendo un polígono, el movimiento resultante de la composición de n movimientos armónicos paralelos puede determinarse con la suma geométrica de los movimientos componentes tales como.
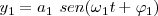
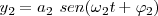
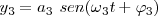

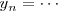
Casos particulares
f1 = f2
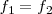
Si suponemos que en una de las vibraciones para 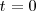
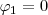 , tenemos,
, tenemos,
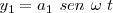
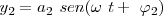
El movimiento resultante depende de la diferencia de fase.
vibraciones en concordancia de fase con 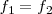
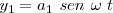
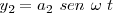
La vibración resultante está en fase con las componentes.
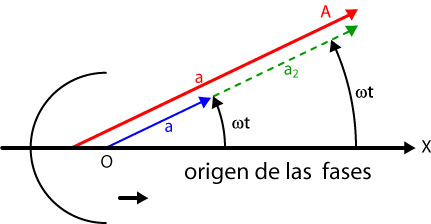
Vibraciones con f1 = f2 y en oposición de fase</math>
Una vibración tendrá una fase 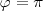
Las ecuaciones de las vibraciones componentes son
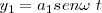
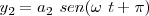
La figura nos muestra que 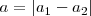 y la vibración resultante esta en fase con la vibración componente de mayor amplitud.
y la vibración resultante esta en fase con la vibración componente de mayor amplitud.
Por otra parte,
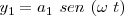
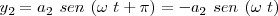
podemos poner el vector 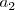 en fase con el anterior pero con sentido opuesto.
en fase con el anterior pero con sentido opuesto.
Vibraciones con f1 = f2 en cuadratura
Dos vibraciones están en cuadratura cuando su diferencia de fase es 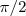 .
.
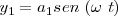
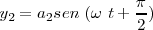
La vibración resultante tendrá por ecuación 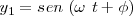 La amplitud a puede calcularse mediante el teorema de Pitágoras
La amplitud a puede calcularse mediante el teorema de Pitágoras
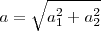
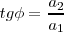
Describe un círculo de radio a.
Veremos después, con más detenimiento este caso al estudiar las figuras de Lissajous
Vibraciones con f1 = f2 con una diferencia de fase φ cualquiera
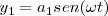
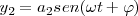
La vibración resultante deberá tener como ecuación 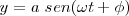
Si tenemos en cuenta el teorema del coseno:
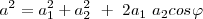
por lo tanto, la amplitud será :
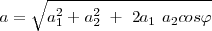
Por otra parte del triángulo 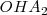 se deduce
se deduce
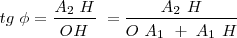
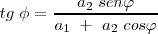
Vemos pues que el ángulo 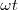 es sólo una mera referencia pues no interviene en al valor de
es sólo una mera referencia pues no interviene en al valor de  .
.
Composición de dos movimientos armónicos de igual dirección y diferente frecuencia
Este fenómeno produce batidos o pulsaciones, que se estudia con detalle en otro archivo
Composiciones de movimientos oscilatorios perpendiculares. - Figuras de Lissajous
Consideremos el caso de una partícula que se mueve en el plano 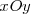 , de tal modo que sus proyecciones sobre los ejes
, de tal modo que sus proyecciones sobre los ejes 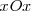 e
e 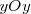 oscilan con movimiento armónico.
oscilan con movimiento armónico.
Caso en que 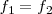
El caso más sencillo sería la composición de dos movimientos cuyas ecuaciones fueran
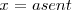
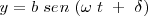 siendo
siendo 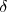 la diferencia de fase.
la diferencia de fase.
La trayectoria de la partícula estaría restringida al rectángulo 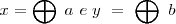 Consideremos el caso en el que
Consideremos el caso en el que 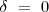 , tenemos:
, tenemos:
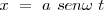
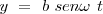
Al dividir una ecuación por otra queda 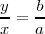 que es la ecuación de una recta de pendiente b/a, que sería la diagonal de un
rectángulo de lado horizontal 2 a y de lado vertical 2b, sobre la que oscilaría el
movimiento resultante.
que es la ecuación de una recta de pendiente b/a, que sería la diagonal de un
rectángulo de lado horizontal 2 a y de lado vertical 2b, sobre la que oscilaría el
movimiento resultante.
La amplitud sería igual 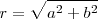
Si los movimientos estuvieran en oposición de fase, 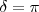 , tenemos
, tenemos
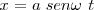
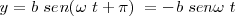
con lo cual:
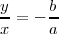
Cuando 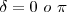 la interferencia de dos movimientos armónicos simples de igual frecuencia producen una polarización rectilínea.
la interferencia de dos movimientos armónicos simples de igual frecuencia producen una polarización rectilínea.
Si las dos movimientos son de igual amplitud y 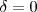
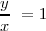
Que es la diagonal de un cuadrado de lado a.
Si 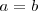 y, además,
y, además, 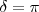 tenemos
tenemos 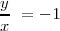
Si 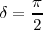
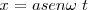
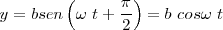
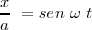
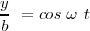
Elevando al cuadrado y sumando tenemos
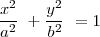
que es la ecuación de una elipse.
En el caso de que 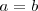 , queda
, queda 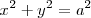 que es la ecuación de una circunferencia.
que es la ecuación de una circunferencia.
El sentido de giro del movimiento al describir la elipse nos viene dado por el valor de la pendiente de la tangente en  , que es la velocidad.
, que es la velocidad.
En  tenemos
tenemos 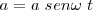 , con lo cual
, con lo cual 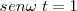
Derivando y con respecto 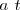



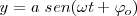
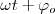 es la fase en el instante
es la fase en el instante 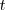
 .
.
 , el radiovector forma un ángulo con el eje de abcisas – origen de referencia para las fases - igual a
, el radiovector forma un ángulo con el eje de abcisas – origen de referencia para las fases - igual a