Ley fundamental de la Dinámica

De Wikillerato

(Diferencias entre revisiones)

Revisión de 11:14 18 jun 2008

Fuerza y cantidad de movimiento

Cuando un sistema, cuya masa supondremos concentrada en su centro de inercia, es sometido a la acción de fuerzas exteriores que no se compensan entre sí , su vector velocidad varía. Si el cuerpo se encontraba en reposo se pondrá en movimiento, y si se encontraba en movimiento se modifica su vector velocidad.

Se llama fuerza a una acción mecánica que conlleva una variación de la cantidad de movimiento del sistema.

Relación fundamental de la dinámica

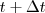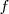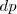Si en un instante t muy próximo a $t + \Delta t$ , un móvil es sometido a la acción de una fuerza $f$ en ese instante $t$ , la variación de la cantidad de movimiento $dp$ tiene la misma dirección y sentido que 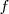$f$ . Dado que 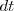$dt$ es un escalar y siempre positivo, el vector 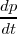$\frac{dp}{dt}$ tiene, además de la misma dirección y sentido, el mismo módulo que 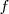$f$ . Podemos pues decir que la fuerza aplicada f es igual a la variación temporal del vector cantidad de movimiento.

$\vec f = \frac {d \vec p} {dt}$

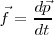
Si el sólido es sometido a la acción de diversas fuerzas cuya suma vectorial es $\sum f$ podremos escribir igualmente

$\sum \vec f \ = \frac {d \vec p} {dt}$

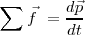
Esta afirmación que no demostramos en este momento es, sin embargo, verificada en numerosos fenómenos. Newton la utilizó para interpretar con éxito las leyes de Kepler referidas al movimiento de los planetas del sistema solar. Esta ley tiene pues el carácter de un postulado conocido como la ley fundamental de la dinámica, bien entendido de la mecanica newtoniana.

En un sistema referencial galileano, la suma vectorial de las fuerzas aplicadas a un sólidoes igual a la derivada con respecto al tiempo del vector cantdad de movimiento del ese sólido.

Aceleración del centro de inercia. Teorema del Centro de Inercia

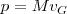Si sustituímos $p$ por su valor $p = M v_G$ y calculamos su derivada, dado que la masa 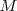$M$ es una constante y la aceleración es la derivada de la velocidad con relación al tiempo, tenemos:

$\sum \vec f \ = \frac {d \vec p} {dt} \ = \frac {d (M \overrightarrow {v_G})}{dt} \ = M \frac {d \overrightarrow {v_G}} {dt} \$

$\sum \vec f \ = M \frac {d \overrightarrow {v_G} } {dt} \ = \ M \overrightarrow {a_G} \$

$\vec F \ = M \overrightarrow {a_G} \$

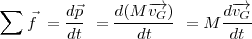
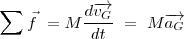
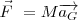
Teorema del centro de inercia: En un sistema referencial galileano, la suma vectorial de las fuerzas aplicadas a un sólido es igual al producto de su masa por el vector aceleración de su centro de inercia.

Atención

Al hallar la suma vectorial de las fuerzas aplicadas sobre el sólido no debemos olvidar nunca el pso P del mismo.

Para obtener el vector aceleración del centro de inercia del sólido, consideramos que toda la masa del sólido se encuentra concentrada en ese punto y aplicamos sobre el mismo el conjunto de fuerzas que se ejercen sobre el sólido. Hablamos de un cuerpo puntual

Obtenido de "http://wikillerato.org/Ley_fundamental_de_la_Din%C3%A1mica.html"