Navegación
Triángulos
De Wikillerato
(→Puntos y rectas notables de los triángulos) |
|||
| Línea 11: | Línea 11: | ||
las bisectrices, <math>b_A , b_B , b_C</math>, que se cortan en el incentro <math>I</math>, centro de la circunferencia inscrita del triángulo; | las bisectrices, <math>b_A , b_B , b_C</math>, que se cortan en el incentro <math>I</math>, centro de la circunferencia inscrita del triángulo; | ||
las alturas, <math>h_A ,h_B , h_C</math>, que se cortan en el ortocentro, <math> \ O \ </math>. | las alturas, <math>h_A ,h_B , h_C</math>, que se cortan en el ortocentro, <math> \ O \ </math>. | ||
| + | |||
| + | |||
[[Imagen:13Triangulos.gif]] | [[Imagen:13Triangulos.gif]] | ||
Revisión de 13:36 28 jul 2008
Características generales
Un triángulo 
es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos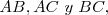 
que son los lados del triángulo. Para que tres segmentos formen un triángulo es necesario que cada uno de ellos sea menor que la suma de los otros dos y mayor que su diferencia.
Puntos y rectas notables de los triángulos
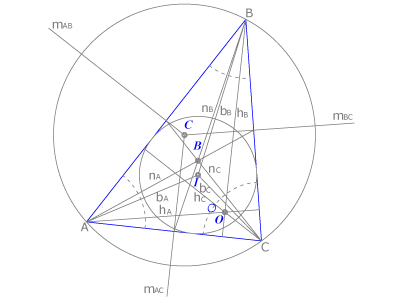
Las rectas y puntos notables de un triángulo ABC son:
las mediatrices, [Unparseable or potentially dangerous latex formula. Error 3 ], que se cortan en un punto llamado circuncentro 
,centro de la circunferencia circunscrita al triángulo;
las medianas,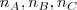 
, que se cortan en el baricentro, 
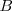, centro de gravedad del triángulo;
las bisectrices, [Unparseable or potentially dangerous latex formula. Error 3 ], que se cortan en el incentro 
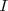, centro de la circunferencia inscrita del triángulo;
las alturas,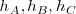 
, que se cortan en el ortocentro, [Unparseable or potentially dangerous latex formula. Error 3 ].
