Navegación
Curvas cónicas
De Wikillerato
(→Intersecciones de rectas y cónicas) |
|||
| Línea 27: | Línea 27: | ||
[[Imagen:40Curvasconicas.gif]] | [[Imagen:40Curvasconicas.gif]] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión de 09:00 6 ago 2008
Tabla de contenidos |
Características generales
Las curvas cónicas son las secciones planas de un cono de revolución.
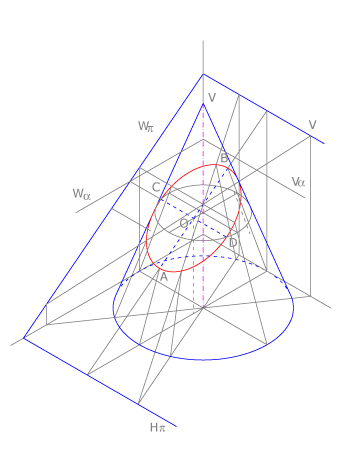
Elipses
La elipse es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es oblicuo al eje y a las generatrices.
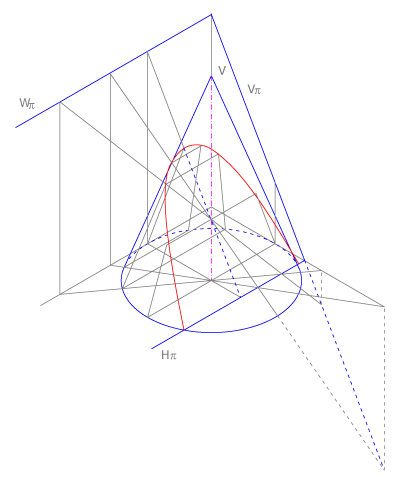
Parábolas
La parábola es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es paralelo a una de las generatrices.
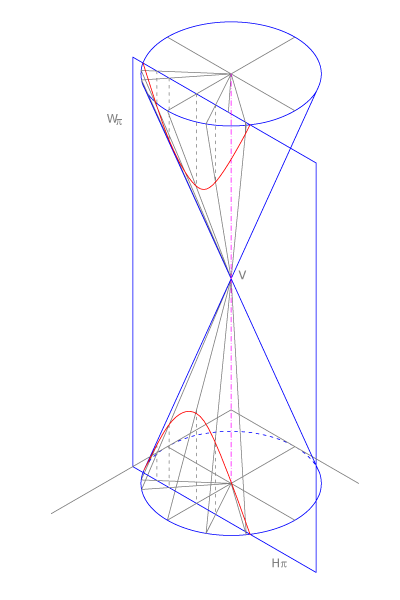
Hipérbolas
La hipérbola es la sección de un cono de revolución con un plano que corta sus dos ramas y que es paralelo al eje del cono.
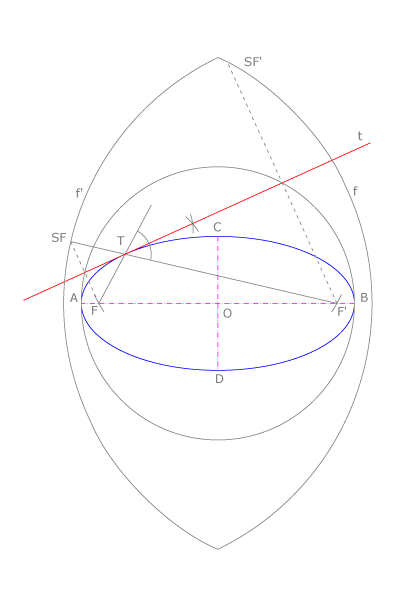
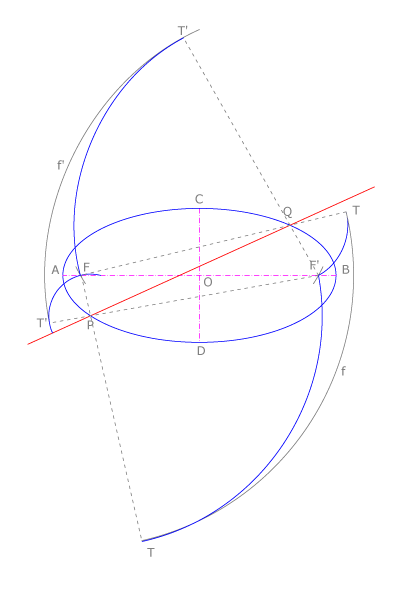
Rectas tangentes a las cónicas
La recta 
tangente a una cónica en un punto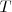 
de la misma es bisectriz del ángulo 
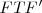, siendo 
y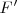 
los focos de la curva. El punto 
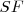, simétrico del foco respecto está sobre la circunferencia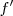 
, focal de 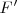. Del mismo modo, 
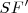está sobre 
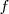, focal de .
Intersecciones de rectas y cónicas
Los puntos 
y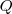 
, intersección de la recta 
con una cónica, son los centros de las circunferencias que pasan por uno de los focos y son tangentes a la focal del otro foco.
En la figura vemos que es centro de dos circunferencias: la que pasa por y es tangente en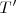 
a la focal de 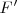y la que pasa por 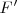y es tangente en 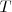a la focal de . Sucede otro tanto con .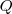
