Navegación
Curvas cónicas
De Wikillerato
(Inserción de ejercicios resueltos en "Enlaces Externos") |
(→Elipses) |
||
| Línea 4: | Línea 4: | ||
Las curvas cónicas son las secciones planas de un cono de revolución. | Las curvas cónicas son las secciones planas de un cono de revolución. | ||
| - | ===Elipses=== | + | '''Texto en negrita'''''Texto en cursiva''[[Título del enlace]]===Elipses=== |
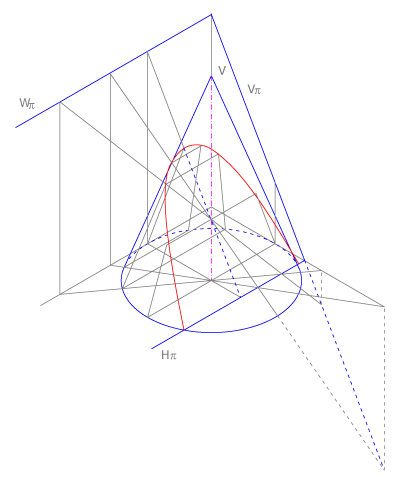
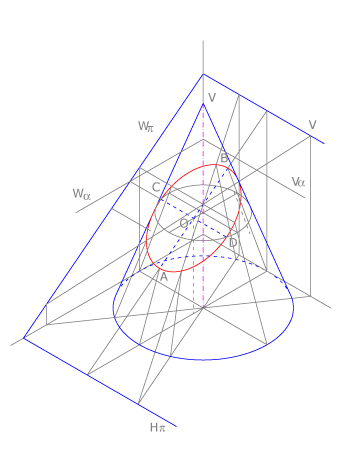
La elipse es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es oblicuo al eje y a las generatrices. | La elipse es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es oblicuo al eje y a las generatrices. | ||
[[Imagen:36Curvasconicas.gif]] | [[Imagen:36Curvasconicas.gif]] | ||
| + | --[[Especial:Contributions/87.217.62.24|87.217.62.24]] 15:13 3 dic 2008 (UTC) | ||
| + | ---- | ||
===Parábolas=== | ===Parábolas=== | ||
Revisión de 15:13 3 dic 2008
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Características generales
Las curvas cónicas son las secciones planas de un cono de revolución.
Texto en negritaTexto en cursivaTítulo del enlace===Elipses=== La elipse es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es oblicuo al eje y a las generatrices.
--87.217.62.24 15:13 3 dic 2008 (UTC)
Parábolas
La parábola es la sección de un cono de revolución con un plano que corta sólo una de sus ramas y que es paralelo a una de las generatrices.
Hipérbolas
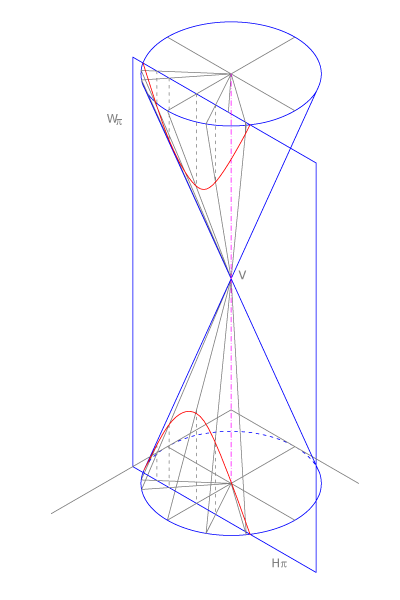
La hipérbola es la sección de un cono de revolución con un plano que corta sus dos ramas y que es paralelo al eje del cono.
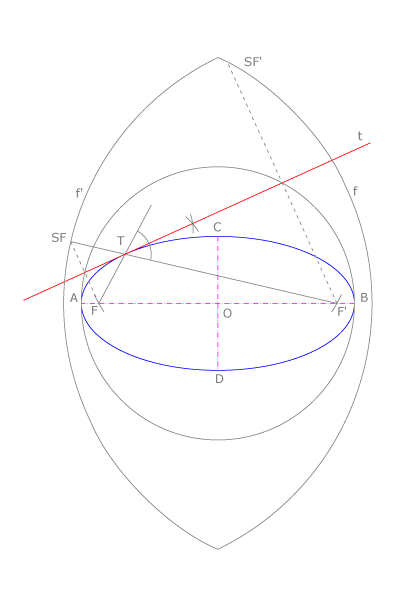
Rectas tangentes a las cónicas
La recta 
tangente a una cónica en un punto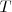 
de la misma es bisectriz del ángulo 
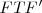, siendo 
y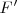 
los focos de la curva. El punto 
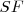, simétrico del foco respecto está sobre la circunferencia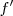 
, focal de 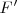. Del mismo modo, 
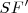está sobre 
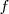, focal de .
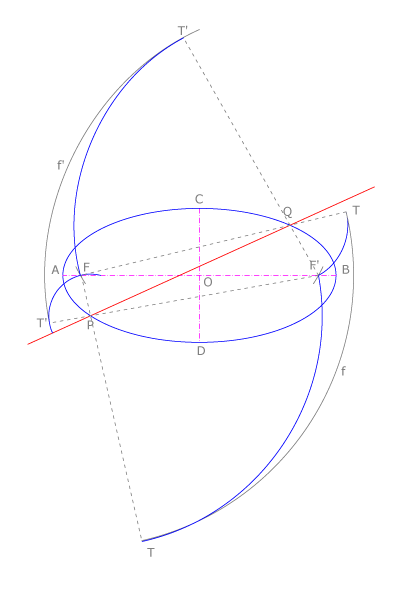
Intersecciones de rectas y cónicas
Los puntos 
y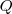 
, intersección de la recta 
con una cónica, son los centros de las circunferencias que pasan por uno de los focos y son tangentes a la focal del otro foco.
En la figura vemos que es centro de dos circunferencias: la que pasa por y es tangente en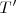 
a la focal de 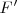y la que pasa por 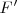y es tangente en 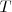a la focal de . Sucede otro tanto con .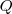
Enlaces Externos
- Problemas de Selectividad resueltos
- Asintotas de una hipérbola definida por sus focos y un punto P de la misma
- Asíntotas de una hipérbola definida por sus focos y una tangente t
- Circunferencia tangente a una recta
- Circunferencias tangentes comunes a una recta y a otra circunferencia, conociendo el punto de tangencia T
- Intersección de una recta con una elipse
- Intersección recta-parábola
- Parábola definida por la directriz y dos rectas tangentes
- Parábola definida por su foco, una tangente y el eje
- Parábola definida por su foco, una tangente y el punto de tangencia
- Rectas tangentes a una elipse desde un punto exterior a la curva
