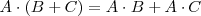Operaciones elementales con matrices
De Wikillerato
(→Suma de matrices) |
m (Revertidas las ediciones realizadas por 190.22.157.23 (Talk); a la última edición de Laura.2mdc) |
||
| Línea 1: | Línea 1: | ||
<br/> | <br/> | ||
| - | ==Suma de | + | ==Suma de matrices== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Para dos [[¿Qué es una matriz?| matrices]] | ||
| + | <math> | ||
| + | A = \left( a_{ij} \right) | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | B = \left( b_{ij} \right) | ||
| + | </math> | ||
| + | de la misma dimensión | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | , la suma de | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | B | ||
| + | </math> | ||
| + | es la matriz de la misma dimensión | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | , dada por | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + B = \left( a_{ij} \right) + \left( b_{ij} \right) = \left( a_{ij} + b_{ij} \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ====Ejemplo==== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + B = | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | a_{11 }& a_{12} & a_{13} | ||
| + | \\ | ||
| + | a_{21 }& a_{22} & a_{23} | ||
| + | \\ | ||
| + | a_{31 }& a_{32} & a_{33} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | + | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | b_{11 }& b_{12} & b_{13} | ||
| + | \\ | ||
| + | b_{21 }& b_{22} & b_{23} | ||
| + | \\ | ||
| + | b_{31 }& b_{32} & b_{33} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13} | ||
| + | \\ | ||
| + | a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23} | ||
| + | \\ | ||
| + | a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Propiedades de la suma de matrices=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 1. Asociativa | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + | ||
| + | \left( | ||
| + | B + C | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | A + B | ||
| + | \right) | ||
| + | + C | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 2. Elemento neutro. La matriz nula, | ||
| + | <math> | ||
| + | 0, | ||
| + | </math> | ||
| + | de la dimension correspondiente es el elemento neutro para la suma, ya que: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + 0 = 0 + A = A | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 3. Elemento opuesto. Para la matriz | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | | ||
| + | existe otra matriz que denotamos por | ||
| + | <math> | ||
| + | -A | ||
| + | </math> | ||
| + | y que llamamos matriz opuesta de | ||
| + | <math> | ||
| + | A, | ||
| + | </math> | ||
| + | que cumple: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + | ||
| + | \left( | ||
| + | -A | ||
| + | \right) | ||
| + | = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 4. Comutativa | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + B = B + A | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
==Producto de un numero por una matriz== | ==Producto de un numero por una matriz== | ||
| Línea 76: | Línea 236: | ||
<br/> | <br/> | ||
| - | ==Producto de | + | ==Producto de matrices== |
| + | |||
| + | <br/> | ||
| + | |||
| + | El producto de dos matrices | ||
| + | <math> | ||
| + | A = \left( a_{ij} \right) | ||
| + | </math> | ||
| + | de dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | B = \left( b_{ij} \right) | ||
| + | </math> | ||
| + | de dimension | ||
| + | <math> | ||
| + | n \times p | ||
| + | </math> | ||
| + | , es la matriz | ||
| + | <math> | ||
| + | A \cdot B | ||
| + | </math> | ||
| + | dada por: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
A \cdot B = \left( c_{ij} \right) | A \cdot B = \left( c_{ij} \right) | ||
| Línea 86: | Línea 274: | ||
con | con | ||
| - | <br/> | + | <br/> |
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | c_{ij} = \sum_{j = 1}^n a_{ij} \cdot b_{jk} | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
Revisión de 08:05 4 dic 2008
Tabla de contenidos |
Suma de matrices
Para dos matrices
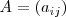 y
y
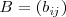 de la misma dimensión
de la misma dimensión
 , la suma de
, la suma de
 y
y
 es la matriz de la misma dimensión
es la matriz de la misma dimensión
 , dada por
, dada por
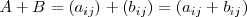
Ejemplo
![A + B =
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 }& a_{12} & a_{13}
\\
a_{21 }& a_{22} & a_{23}
\\
a_{31 }& a_{32} & a_{33}
\end{array}
</pre>
<p>\right)
+
\left(
</p>
<pre> \begin{array}[c]{ccc}
b_{11 }& b_{12} & b_{13}
\\
b_{21 }& b_{22} & b_{23}
\\
b_{31 }& b_{32} & b_{33}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
\\
a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
\\
a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
\end{array}
</pre>
<p>\right)
A + B =
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 }& a_{12} & a_{13}
\\
a_{21 }& a_{22} & a_{23}
\\
a_{31 }& a_{32} & a_{33}
\end{array}
</pre>
<p>\right)
+
\left(
</p>
<pre> \begin{array}[c]{ccc}
b_{11 }& b_{12} & b_{13}
\\
b_{21 }& b_{22} & b_{23}
\\
b_{31 }& b_{32} & b_{33}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
\\
a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
\\
a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
\end{array}
</pre>
<p>\right)](/images/math/math-83b07e70030828d73f75b5a4cd132a90.png)
Propiedades de la suma de matrices
1. Asociativa
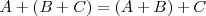
2. Elemento neutro. La matriz nula,
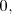 de la dimension correspondiente es el elemento neutro para la suma, ya que:
de la dimension correspondiente es el elemento neutro para la suma, ya que:
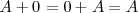
3. Elemento opuesto. Para la matriz
 existe otra matriz que denotamos por
existe otra matriz que denotamos por
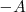 y que llamamos matriz opuesta de
y que llamamos matriz opuesta de
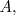 que cumple:
que cumple:
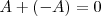
4. Comutativa
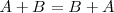
Producto de un numero por una matriz
Para un número real
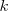 y una matriz
y una matriz
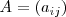 de dimension
de dimension
 , el producto de un número real por una matriz es la matriz de la misma dimension
, el producto de un número real por una matriz es la matriz de la misma dimension
 dada por
dada por
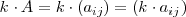
Es decir, el producto
 se obtiene multiplicando el numero real por cada uno de los elementos de la
matriz.
se obtiene multiplicando el numero real por cada uno de los elementos de la
matriz.
Ejemplo
![k \cdot A = k \cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11 }& a_{12}
\\
a_{21 }& a_{22}
\\
a_{31 }& a_{32}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
k \cdot a_{11 }& k \cdot a_{12}
\\
k \cdot a_{21 }& k \cdot a_{22}
\\
k \cdot a_{31 }& k \cdot a_{32}
\end{array}
</pre>
<p>\right)
k \cdot A = k \cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11 }& a_{12}
\\
a_{21 }& a_{22}
\\
a_{31 }& a_{32}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
k \cdot a_{11 }& k \cdot a_{12}
\\
k \cdot a_{21 }& k \cdot a_{22}
\\
k \cdot a_{31 }& k \cdot a_{32}
\end{array}
</pre>
<p>\right)](/images/math/math-ac0775a178d76f16f0d842a39ec92976.png)
Producto de matrices
El producto de dos matrices
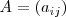 de dimension
de dimension
 y
y
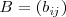 de dimension
de dimension
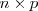 , es la matriz
, es la matriz
 dada por:
dada por:
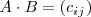
con
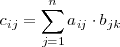
Es decir, cada elemento
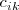 se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
k-ésima de la segunda matriz.
se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
k-ésima de la segunda matriz.
Ejemplo
![\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
4 & 5 & 6
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
~~7 & ~~8
\\
~~9 & ~~0
\\
-1 & -2
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
\\
4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
4 & 5 & 6
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
~~7 & ~~8
\\
~~9 & ~~0
\\
-1 & -2
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
\\
4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
\end{array}
</pre>
<p>\right)](/images/math/math-2ff8eff26cdd9448d6141d459441e2d9.png)
Propiedades del producto de matrices
1. El producto de matrices cuadradas es asociativo:
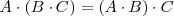
2. El producto de matrices cuadradas de orden
 posee como elemento neutro la matriz unidad o identidad
posee como elemento neutro la matriz unidad o identidad
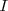 de orden
de orden
 ya que:
ya que:
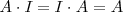
3. El producto de matrices cuadradas es distributivo respecto de la suma de matrices: