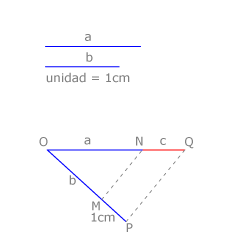
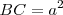El teorema de Euclides

De Wikillerato

(Diferencias entre revisiones)

Revisión de 15:06 27 ene 2009

Ya vimos el teorema de Euclides, considerando su enunciados como teoremas de la altura y del cateto, en el capítulo de triángulos y realizamos sus demostraciones gráficas.

Ahora vamos a ver su relación con la tercera proporcional. Si consideramos que:

$\frac{a}{x}=\frac{x}{b}$

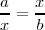
vemos que el término intermedio, x, es media proporcional entre a y b, pues:

$x^2 = ab$

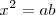
Las construcciones de la media proporcional de dos segmentos, basadas directamente en Euclides, tienen muchas aplicaciones en la resolución de problemas gráficos.

Tabla de contenidos

1 Aplicando el teorema de la altura

Aplicando el teorema de la altura

Dibujamos el segmento BC= a+b, como vemos en la figura. Trazamos la semicircunferencia de diámetro BC. Por el extremo común de los segmentos, H, dibujamos la perpendicular a BC que corta al arco en A. AH es la altura de ABC y es media proporcional de los segmentos en que divide a la hipotenusa: a y b, como ya vimos en el capítulo 2.

$AH = \sqrt{ab}$

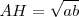
Aplicando el teorema del cateto

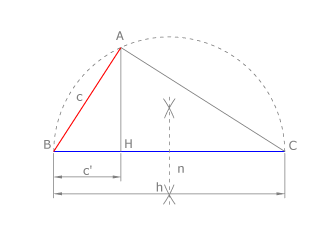
Dibujamos el segmento BC=b y BH=a, superpuestos, como vemos en la figura. Trazamos la semicircunferencia de diámetro BC. La perpendicular a BC desde H corta al arco en A.

El cateto AB es media proporcional su proyección sobre la hipotenusa, a , y de la hipotenusa, b, como ya vimos en el capítulo 2.

$AB = \sqrt{ab}$

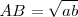
Aplicaciones al cálculo gráfico

Para resolver estos problemas debemos definir la unidad que consideramos.

División de dos segmentos: c=a/b

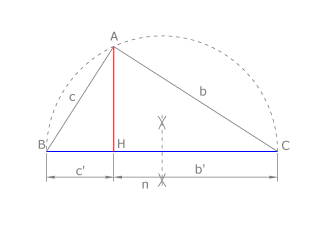
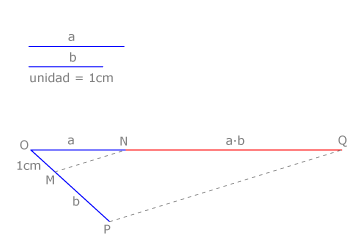
Dados los segmentos a y b hallamos un tercer segmento c que cumpla: c=a/b, siendo la unidad el centímetro.

Dibujamos un haz de dos rectas que se cortan en O. Sobre una de ellas llevamos ON=a y sobre la otra OM=b y MP=1cm (segmento unidad), como vemos en la figura. Dibujamos MN y su paralela por P, PQ.

$NQ=c$

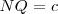
Vemos que se cumple:

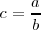$c=\frac{a}{b}$ pues:

$\frac{a}{b}=\frac{c}{1}$

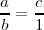
Producto de dos segmentos: c=ab

Dados los segmentos a y b hallamos un tercer segmento c que cumpla: c=ab, siendo la unidad el centímetro.

Dibujamos un haz de dos rectas que se cortan en O. Sobre una de ellas llevamos ON=a y sobre la otra OM=1cm (segmento unidad) y MP=b, como vemos en la figura. Dibujamos MN y su paralela por P, PQ.

$NQ=c$

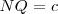
Vemos que se cumple:

$c=ab$

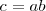
pues:

$\frac{a}{1}=\frac{c}{b}$

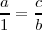
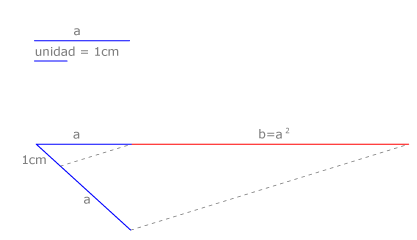
Cuadrado de un segmento: b=a²

Dado un segmento a hallamos un segmento b que cumpla 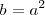$b=a^2$ , siendo la unidad el centímetro.

Esta construcción una variante de la del producto de un segmento.

Dibujamos un haz de dos rectas que se cortan en O. Sobre una de ellas llevamos ON=a y sobre la otra OM=1cm (segmento unidad) y MP=a, como vemos en la figura. Dibujamos MN y su paralela por P, PQ.

$NQ=b$

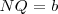
Vemos que se cumple:

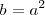$b=a^2$ ,pues:

$\frac{a}{1} = \frac{b}{a}$

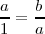
Raíz cuadrada de un segmento: b=√a

Dado un segmento a hallamos un segmento b que cumpla 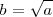$b= \sqrt{a}$ , siendo la unidad el centímetro

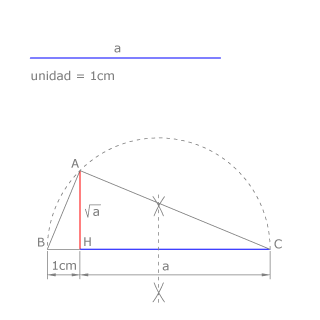
Aplicamos el teorema de la altura:

Dibujamos el segmento BC, siendo BH = 1cm (segmento unidad) y HC=a.

Trazamos la semicircunferencia de diámetro BC. La perpendicular a BC por H corta al arco en A.

$AH =b = \sqrt{a}$

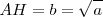
pues b es media proporcional de a y de la unidad.

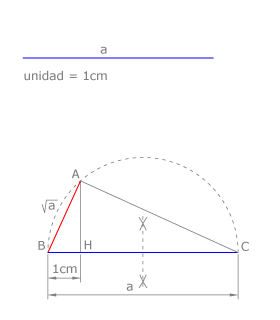
Esta construcción también se hace aplicando el teorema del cateto, como puede verse en la figura.

En este caso se dibuja el segmento BH=1cm y el segmento BC=a.

Dibujamos la circunferencia de diámetro BC. Trazamos la perpendicular a BC desde H. Esta recta corta a la circunferencia en A.

La magnitud solución es 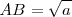$AB = \sqrt{a}$

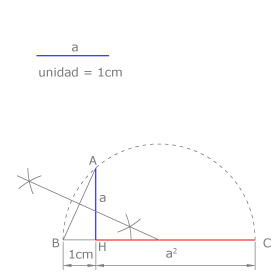
Cuadrado de un segmento, aplicando Euclides

Aplicamos el teorema de la altura:

Dibujamos el segmento BH = 1cm (segmento unidad) y prolongamos la recta que lo contiene.

Trazamos la perpendicular a BH por H y llevamos la magnitud a sobre ella:

$AH = a$

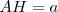
Dibujamos el arco de circunferencia que pasa por A y B y tiene el centro en la recta definida por BH. Su centro estará en la intersección de la mediatriz de AB con dicha recta. El arco corta a la recta en C.

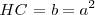$HC= b = a^2$ , pues 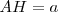$AH=a$ es media proporcional de 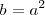$b=a^2$ y de la unidad.

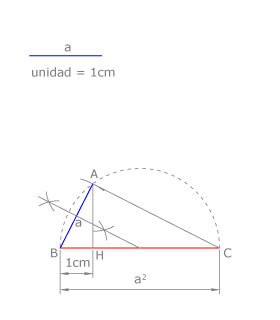
Esta construcción también se hace aplicando el teorema del cateto, como puede verse en la figura. En este caso se dibuja el segmento BH=1cm y se prolonga la recta que lo contiene. Se dibuja la perpendicular a dicha recta desde H y, con centro en B y radio a se traza el arco que la corta en A.

Dibujamos la circunferencia que pasa por A y B y tiene el centro en la recta BH: trazamos la mediatriz de AB que corta a dicha recta en su centro.

BC es la magnitud solución: $BC=a^2$