Navegación
Propiedades de las integrales indefinidas
De Wikillerato
(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 201.220.44.9 (Talk); a la última edición de Laura.2mdc) |
|||
| Línea 51: | Línea 51: | ||
ambas igualdades. | ambas igualdades. | ||
| - | [[Categoría:Matemáticas]] | + | [[Categoría:Matemáticas]] |
| - | + | ||
Revisión de 07:28 5 may 2009
Por la definición, la derivada de la función integral indefinida es igual a la función integrando:
![\left[
</p>
<pre> \, \int \mathrm{f} \left( \, x \, \right) \mathrm{d}x \,
</pre>
<p>\right]
^\prime \, = \, \mathrm{f} \left( \, x \, \right)](/images/math/math-c06a2d0283cdfe91518030ef55eefff0.png "\left[
</p>
<pre> \, \int \mathrm{f} \left( \, x \, \right) \mathrm{d}x \,
</pre>
<p>\right]
^\prime \, = \, \mathrm{f} \left( \, x \, \right)")
La integral de la suma de dos funciones es igual a la suma de las integrales de las funciones:
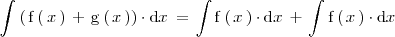
La integral indefinida del producto de un número real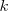 
por una función es igual al producto de 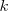por la integral indefinida de la función:
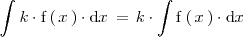
Para demostrar las ultimas dos igualdades basta con derivar los dos terminos en ambas igualdades.
Tweet
