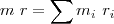Ley de inercia. Masa de un cuerpo
De Wikillerato
(→La masa) |
(→La densidad) |
||
| Línea 198: | Línea 198: | ||
| - | Es bien conocida la pregunta | + | Es bien conocida la pregunta: ¿qué pesa más un hilo de paja o un kilo de hierro? Esta pregunta así expresada carece de total interés, pero se traduce en una observación común: un cierto volumen de paja es más ligero que si cargamos con el mismo volumen de hierro. Estas características de los cuerpos que los diferencia, se expresan por dos nociones, la densidad absoluta ρ, que se define como la masa del cuerpo por unidad de volumen, o la densidad relativa, que se expresa mediante el cociente de las masas respectivas que hay en dos volúmenes iguales. |
| - | + | ||
====Densidad absoluta==== | ====Densidad absoluta==== | ||
| Línea 235: | Línea 234: | ||
<math>densidad \ relativa = \frac {\rho} {\rho_0} \ </math> | <math>densidad \ relativa = \frac {\rho} {\rho_0} \ </math> | ||
| - | |||
===Centros de Inercia de dos sólidos=== | ===Centros de Inercia de dos sólidos=== | ||
Revisión de 05:03 15 sep 2009
Tabla de contenidos |
Sistemas sólidos
En mecánica un sólido es un cuerpo indeformable por lo que recibe también el nombre de sólido rígido.
En un sólido, S, en el que elegimos dos puntos cualesquiera M y N, la distancia MN permanece constante cualquiera que sea el movimiento del cuerpo. Todos sus puntos se encuentran entre sí a distancias invariables. Su forma y su volumen no cambian en curso de su movimiento.
Una bola o un cilindro de acero, de aluminio o de bakelita son buenos ejemplos de sólidos rígidos.
Pero la noción de Sistema entraña una realidad mucho más general pues puede estar formado por varios sólidos, entre los cuales puede ocurrir:
- - Los cuerpos pueden presentar uniones rígidas.
- - Los cuerpos pueden presentar uniones elásticas.
- - Puede no existir unión alguna, o también que la suma de las fuerzas que actúan sobre una parte del cuerpo sea nula y diremos también que esa parte constituye un sistema aislado.
En los ejemplos vistos de las esferas de acero, aluminio o bakelita, las uniones entre las diferentes partes del cuerpo son uniones rígidas.
La unión entre dos masas unidas por un resorte diremos que es elástica.
De un astronauta que se encuentra en el interior de un satélite artificial que describe su órbita decimos que se encuentra en estado de ingravidez porque la suma de las fuerzas que actúan sobre él es cero.
Centro de Inercia de un Sólido
Cuando, en un instante dado, en todos los puntos de un sólido el vector velocidad es el mismo decimos que su movimiento es de traslación. En la cinemática se estudia que si el vector velocidad v es independiente del tiempo, el movimiento del cuerpo es rectilíneo y uniforme.
En un caso más general, un sólido tiene simultáneamente un movimiento de traslación y un movimiento de rotación. Se puede poner como ejemplo la rueda de una bicicleta en movimiento, una regla que se lance en el aire…
Supongamos que al cuerpo anterior lo lanzamos horizontalmente sobre un colchón de aire.
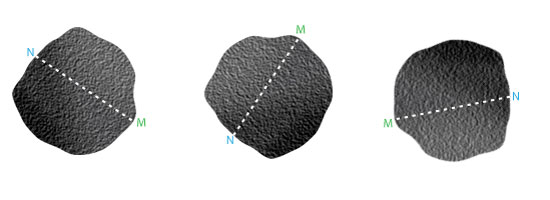
Un colchón de aire es un tablero en el que se han practicado varias centenas de orificios muy pequeños por los que se envía aire a presión. En la parte inferior lleva una caja por la que se inyecta aire a suficiente presión como para poder soportar, levitando, un objeto. El aire sale por todos los orificios a igual presión de acuerdo con el Teorema de Pascual – Todo aumento de presión en un punto en el seno de un fluido da lugar al mismo aumento de presión del fluido en cualquier otro punto del mismo cualquiera la dirección elegida- Los aumentos de presión en todos puntos de contacto del aire a presión del interior a la caja con el aire exterior son iguales en cada orificio, las diferencias de presión interior y exterior serán iguales en cada punto. La obtención del aire a presión es bien sencilla, basta con conectar el motor de un aspirador al revés.
Si lanzamos horizontalmente un objeto plano sobre el que se hayan señalado ciertos puntos, se observa que hay uno, uno sólo, de todos los puntos que se mantiene siempre la misma recta. Es decir, es el único punto del sólido cuyo movimiento es rectilíneo y uniforme. En todo instante el objeto levita, su peso P queda anulado por la presión del aire extendida a toda su superficie, pues 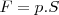 , que equivale a la fuerza de reacción
, que equivale a la fuerza de reacción 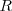 de la mesa si no dispusiese del aire a presión. El sistema podrá considerarse aislado o pseudoaislado. No es igual que no actúe sobre él ninguna fuerza, sistema aislado, que la suma de todas las fuerzas aplicadas sobre el cuerpo es cero.
de la mesa si no dispusiese del aire a presión. El sistema podrá considerarse aislado o pseudoaislado. No es igual que no actúe sobre él ninguna fuerza, sistema aislado, que la suma de todas las fuerzas aplicadas sobre el cuerpo es cero. 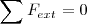 , se comporta como si estuviera aislado pero sin serlo, es pseudoaislado
, se comporta como si estuviera aislado pero sin serlo, es pseudoaislado
Estudiamos el movimiento de un círculo de plexiglás, sobre el que hayamos señalado el centro O del mismo y un punto de su periferia P, dándole un pequeño impulso tangente a la circunferencia, se observa que el centro del círculo O permanece siempre sobre la misma recta, en tanto que el movimiento de M es curvilíneo.
Si empujamos un paralelepípedo, cualquiera que sea la cara sobre la que se apoye, solamente el centro de simetría permanece sobre la misma recta. Su movimiento es rectilíneo.
Llamamos centro de inercia G de un sólido S al punto único del mismo que se moverá con movimiento rectilíneo y uniforme cuando se desplaza sin rozamiento sobre una superficie horizontal, con independencia de las condiciones iniciales del movimiento.
El punto G puede encontrarse fuera del sólido, por ejemplo en un anillo o en un cubo o en un cilindro huecos.
En el caso particular de un movimiento de traslación rectilíneo y uniforme todos los puntos tendrán el mismo movimiento que G.
En un caso más general, el movimiento del sólido puede descomponerse en dos:
- - Un movimiento del conjunto, rectilíneo y uniforme, representado por el que realiza con relación al sistema de referencia escogido
- -Un movimiento propio, representado por el movimiento de un punto cualquiera del sólido alrededor de G.
Determinación de los Centros de Inercia
Centro de simetría de un sólido homogéneo
Una vez aceptado que el sólido es homogéneo, si el sólido posee un eje de simetría o, en su caso, un plano, el centro de simetría pertenecerá al eje de simetría, o al plano, respectivamente. De este modo, podremos considerar G como el punto intersección del eje de simetría y del plano perpendicular a él. Dado que el sólido es homogéneo, el centro de simetría es su centro de inercia.
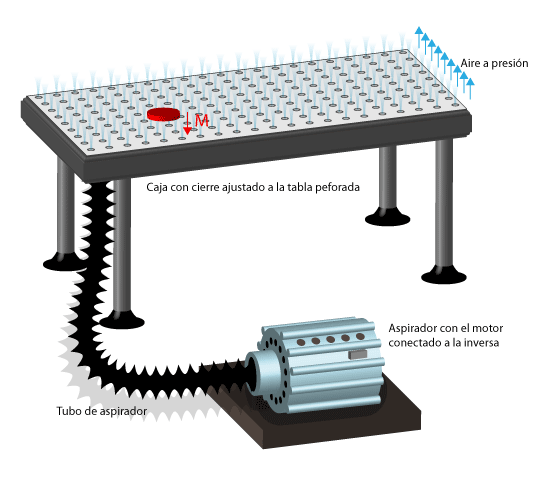
A continuación, se presentan diversos sólidos que se pueden encontrar en los experimentos más usuales, de los que trataremos de determinar sus centros de inercia G.
•Centro de inercia de una placa triangular Es el punto medio del segmento determinado por el baricentro de las dos caras. El baricentro del triángulo es el punto donde se cortan las medianas.
• Centro de inercia de una placa con forma de paralelogramo El punto medio del segmento determinado por los puntos donde se cortan las diagonales de cada cara.
En ambos casos basta con medir el espesor - y dividirlo por dos- y determinar el baricentro del tríángulo y del paralelogramo, respectivamente.
• Centro de inercia de un disco Es el punto medio del segmento determinado por los centros de loas círculos que forman las bases.
• Centro de inercia de un aro Se encuentra fuera del cuerpo, y es el mismo que el del disco macizo.
• Centro de inercia de un prisma Se encuentra en el punto medio del segmento determinado por los centros de simetría de dos bases opuestas.
• Centro de inercia de un cilindro Es el punto medio del segmento determinado por los centros geométricos de las bases.
• Centro de inercia de una esfera Cualquiera que sea la forma en que la esfera ruede el único punto que presentará un movimiento rectilíneo y uniforme es el centro de la esfera.
Sistemas no aislados
Cuando el sistema no es aislado, o 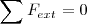 , el movimiento del centro de inercia deja de ser uniforme. Inclinando la mesa sobre la que descansa la
sólido, llega un momento en la que éste comienza a deslizar y a adquirir un movimiento no uniforme.
De igual modo, el movimiento de una bola de billar, debido al rozamiento entre la bola y el tapiz, pierde poco a poco velocidad hasta detenerse.
Sin embargo, podemos conseguir que el sistema mantenga la velocidad constante, aplicándole una fuerza que anula las fuerzas de rozamientos. El sistema es pseudoaislado.
, el movimiento del centro de inercia deja de ser uniforme. Inclinando la mesa sobre la que descansa la
sólido, llega un momento en la que éste comienza a deslizar y a adquirir un movimiento no uniforme.
De igual modo, el movimiento de una bola de billar, debido al rozamiento entre la bola y el tapiz, pierde poco a poco velocidad hasta detenerse.
Sin embargo, podemos conseguir que el sistema mantenga la velocidad constante, aplicándole una fuerza que anula las fuerzas de rozamientos. El sistema es pseudoaislado.
Principio de Inercia
Galileo Galilei enunció, en el siglo XVI, este principio que fue más tarde completado por Newton.Debemos tener en cuenta, que un principio es siempre una proposición, basada o no en experiencias, que se admite sin demostración y de la que se pueden siempre intentar nuevas experiencias que la contradiga pero, en lo que se refiere al principio de inercia, hasta el momento no se ha conseguido encontrar contradicciones. Por esta causa, el principio es admitido como verdad en tanto no se encuentra una falsación. (Véase Kart Popper, Teoría del progreso científico)
El centro de inercia G de un sólido aislado, o cuya 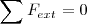 , o permanece inmóvil o tiene un movimiento rectilíneo y uniforme. Es decir si
, o permanece inmóvil o tiene un movimiento rectilíneo y uniforme. Es decir si 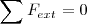 ,
, 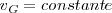
La inercia nos mide la dificultad que tiene un cuerpo para modificar su estado de reposo (es decir de iniciar un movimiento) o de movimiento rectilíneo y uniforme ( es decir, de cambiar de velocidad)
La masa
La masa m de un cuerpo es la magnitud física que nos mide cuantitativamente la inercia de los cuerpos. La masa de un cuerpo dado permanece constante. No depende del lugar donde se encuentre el cuerpo. Ya se ha dicho que dos masas iguales, colocadas sobre sendos platillos de una balanza, se equilibran por igual en la Tierra o en la Luna. Sin embargo su peso depende del lugar donde se encuentre, pues cambia la intensidad del vector gravedad g, y un dinamómetro nos marcaría pesos (fuerzas) diferentes según el lugar donde nos encontremos. En consecuencia, la masa m depende únicamente de la cantidad de materia del cuerpo, el peso depende también del valor que adopte g en el lugar donde se encuentre m –y es una magnitud vectorial, pues tiene la dirección y el sentido de g -. .
La unidad de masa es el kilogramo, kg.
El kilogramo patrón es un cilindro de platino conservado en la Oficina Internacional de Pesos y Medidas, en Sèvres, cerca de París.
Existen múltiplos y submúltiplos del kilogramo, aunque para los trabajos experimentales se utilice más el gramo g.
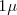
| 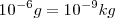
| |
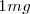
| 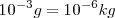
| |
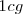
| 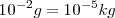
| |
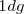
| 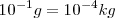
| |
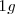
| 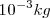
| |
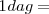
| 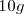
| 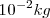
|
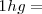
| 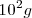
| 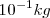
|
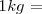
| 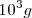
| |
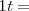
| 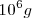
| 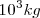
|
La masa se nos presenta bajo dos aspectos fundamentales, un aspecto gravitatorio (todo cuerpo tiene un peso en la superficie de la Tierra) y un aspecto inercial, que caracteriza la propiedad de que existe una dificultad para poner el cuerpo en movimiento o para modificar este movimiento.
La densidad
Es bien conocida la pregunta: ¿qué pesa más un hilo de paja o un kilo de hierro? Esta pregunta así expresada carece de total interés, pero se traduce en una observación común: un cierto volumen de paja es más ligero que si cargamos con el mismo volumen de hierro. Estas características de los cuerpos que los diferencia, se expresan por dos nociones, la densidad absoluta ρ, que se define como la masa del cuerpo por unidad de volumen, o la densidad relativa, que se expresa mediante el cociente de las masas respectivas que hay en dos volúmenes iguales.
Densidad absoluta
Un cuerpo, sea éste sólido, líquido o gas, se caracteriza por su masa m, que depende de la cantidad de materia, pero también lo caracteriza su volumen, V, medido en m3 en el S.I. Así como la cantidad de materia es invariable, el volumen depende de otra serie de circunstancias tales como la temperatura.
Si nos encontramos frente a dos objetos idénticos, los dos de masa m y de volumen V, al considerar el sistema en su conjunto tendrá de masa 2 m y de volumen 2V, sin embargo el cociente entre masa y volumen del conjunto no ha cambiado.
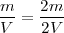
A ese cociente lo llamamos densidad absoluta, o densidad, 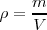
Su unidad en el S.I. es 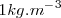 , aunque en la vida cotidiana se utiliza
, aunque en la vida cotidiana se utiliza 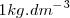 , que se corresponden
, que se corresponden 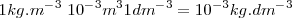
Por otra parte 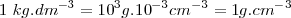
Para el agua 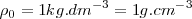
La densidad relativa, d
Es la relación entre la masa de dos cuerpos que ocupan igual volumen. En realidad es el cociente entre sus densidades absolutas.
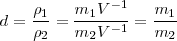
* La densidad de un cuerpo con relación al agua es el cociente entre la masa del cuerpo y la masa del agua, medidas en las mismas condiciones.
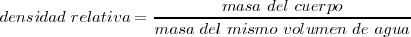
O bien
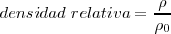
Centros de Inercia de dos sólidos
Si dos sólidos 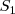 y
y 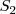 , de masas
, de masas 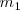 y
y 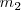 , pueden evolucionar simultáneamente sobre un colchón de aire, cada uno de esos dos sólidos constituye un sistema y posee su propio centro de inercia,
, pueden evolucionar simultáneamente sobre un colchón de aire, cada uno de esos dos sólidos constituye un sistema y posee su propio centro de inercia, 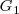 y
y 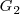 , respectivamente.
, respectivamente.
Sin embargo, si unimos los dos sólidos por algún procedimiento, el resultado es un nuevo sólido 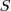 cuya masa
cuya masa 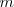 será igual a
será igual a 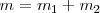 , con su propio centro de inercia
, con su propio centro de inercia 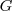 se podrá determinar experimentalmente.
se podrá determinar experimentalmente.
a) Sólidos de igual masa 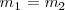
El centro de inercia G de S se encuentra en todo instante en el punto medio del segmento definido por 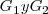
b) Sólidos de masas diferentes 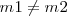
Si tomamos un sistema de referencia 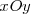 , podremos determinar el centro de masas
, podremos determinar el centro de masas 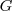 del sólido resultante.
del sólido resultante.
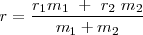
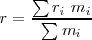
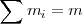 , entonces
, entonces