Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Periodicidad

De Wikillerato

(Diferencias entre revisiones)
(→Ejemplo)
Línea 78: Línea 78:
[[Category:Matemáticas]]
[[Category:Matemáticas]]
 +
 +
 +
<img style="visibility:hidden;width:0px;height:0px;" border=0 width=0 height=0 src="http://counters.gigya.com/wildfire/IMP/CXNID=2000002.0NXC/bT*xJmx*PTEyNjMwODE1MjM1NzgmcHQ9MTI2MzA4MTUyNzcxOCZwPTk3NDcxJmQ9Jmc9MSZvPWE5N2U2NDA5ZmZkMjQzODc4OWExYmYyYjFkNDRjMWI1.gif" />
 +
<p><a href="http://parahi5.com/"><img src="http://src.parahi5.com/graficos/friends/tu_amistad_es_bella.gif" border ="0" title="imagenes para hi5" alt="imagenes para hi5"></a><p><a href="http://parahi5.com/">imagenes para hi5</a><a href="http://src.parahi5.com/"><img src="http://src.parahi5.com/parahi5.gif" title="hi5"></a></p>

Revisión de 01:20 10 ene 2010

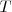Se dice que una función   \mathrm{f}   es periódica, de periodo   T ,   con   [Unparseable or potentially dangerous latex formula. Error 3 ]   y   [Unparseable or potentially dangerous latex formula. Error 3 ] , si verifica que:


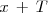1. Si   x   esta en el dominio de   \mathrm{f} , entonces   x \, + \, T   tambien esta en el dominio de   \mathrm{f} .


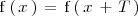2.   \mathrm{f} \left( \, x \, \right) \, = \, \mathrm{f} \left( \, x \, + \, T \, \right)   para todo   x   en el dominio de   \mathrm{f}


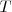3.   T   es el menor número real que cumple esta condición.


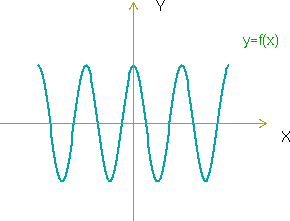
Ejemplo


\mathrm{f} \left( \, x \, \right) \, = \, 1'2 \cdot \cos \left( \, 5x \, \right)


Imagen:coseno.png



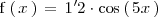
<img style="visibility:hidden;width:0px;height:0px;" border=0 width=0 height=0 src="http://counters.gigya.com/wildfire/IMP/CXNID=2000002.0NXC/bT*xJmx*PTEyNjMwODE1MjM1NzgmcHQ9MTI2MzA4MTUyNzcxOCZwPTk3NDcxJmQ9Jmc9MSZvPWE5N2U2NDA5ZmZkMjQzODc4OWExYmYyYjFkNDRjMWI1.gif" />

<a href="http://parahi5.com/"><img src="http://src.parahi5.com/graficos/friends/tu_amistad_es_bella.gif" border ="0" title="imagenes para hi5" alt="imagenes para hi5"></a><p><a href="http://parahi5.com/">imagenes para hi5</a><a href="http://src.parahi5.com/"><img src="http://src.parahi5.com/parahi5.gif" title="hi5"></a>

Obtenido de "http://wikillerato.org/Periodicidad.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.