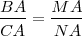Navegación
Proporcionalidad directa
De Wikillerato
(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 190.152.203.171 (Talk); a la última edición de Laura.2mdc) |
(→Características generales) |
||
| Línea 1: | Línea 1: | ||
===Características generales=== | ===Características generales=== | ||
| - | Consideramos que una variable '''x''' puede adquirir los valores '''a,b,c,d,...''' y otra variable los valores '''a' , b' , c' , d' , ...''' '''x''' e '''y''' son directamente proporcionales si | + | Consideramos que una variable '''x''' puede adquirir los valores '''a,b,c,d,...''' y otra variable los valores '''a' , b' , c' , d' , ...''' '''x''' e '''y''' son directamente proporcionales si esta pagina no sirve |
<math>\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'}...</math> | <math>\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'}...</math> | ||
Revisión de 18:43 11 may 2010
Características generales
Consideramos que una variable x puede adquirir los valores a,b,c,d,... y otra variable los valores a' , b' , c' , d' , ... x e y son directamente proporcionales si esta pagina no sirve
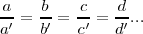
Teorema de Tales
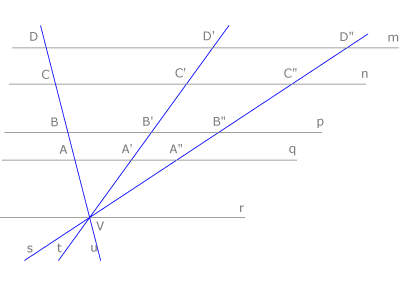
Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas:
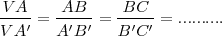
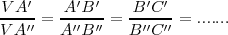
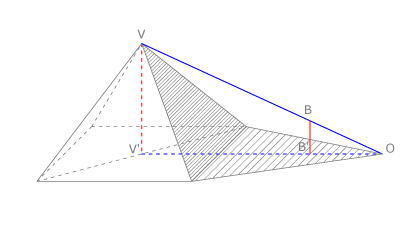
En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón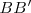 
.
En nuestra figura vemos que la altura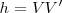 
es la incógnita de esta igualdad:
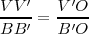, luego
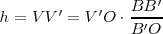
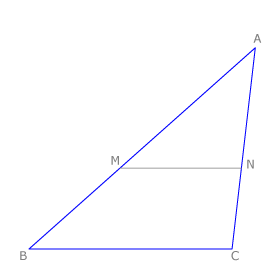
El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que:
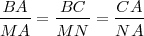
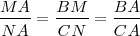
De la primera igualdad deducimos la segunda ya que:
