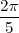Periodicidad
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
Se dice que una función | Se dice que una función | ||
<math> | <math> | ||
| Línea 13: | Línea 11: | ||
T > 0 | T > 0 | ||
</math> | </math> | ||
| - | , si verifica | + | , si y solo si verifica las siguientes dos condiciones: |
<br/> | <br/> | ||
| - | 1. | + | 1. |
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) \, = \, \mathrm{f} \left( \, x \, + \, T \, \right) | ||
| + | </math> | ||
| + | para todo número real | ||
<math> | <math> | ||
x | x | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 2. | ||
| + | <math> | ||
| + | T | ||
</math> | </math> | ||
| - | | + | es el menor número positivo que cumple la anterior condición. |
| + | |||
| + | <br/> | ||
| + | |||
| + | Tipicas funciones periodicas son las funciones trigonometricas: el coseno, el | ||
| + | seno y la tangente. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Son funciones periodicas | ||
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | \left\{ |
| - | </math> | + | \begin{array}{l} |
| - | + | f \left( \, x \, \right) = a \cdot cos ( b \cdot x + c ) | |
| + | \\ | ||
| + | g \left( \, x \, \right) = a \cdot sen ( b \cdot x + c ) | ||
| + | \\ | ||
| + | h \left( \, x \, \right) = a \cdot tan ( b \cdot x + c ) | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | donde | ||
<math> | <math> | ||
| - | + | a | |
</math> | </math> | ||
| - | + | , | |
<math> | <math> | ||
| - | + | b | |
| - | </math>. | + | </math> |
| + | y | ||
| + | <math> | ||
| + | c | ||
| + | </math> | ||
| + | son numeros reales cualesquiera. | ||
<br/> | <br/> | ||
| - | + | Una funci\'on constante es una funci\'on periodica. | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Para determinar completamente una funci\'on periodica de periodo | ||
<math> | <math> | ||
| - | + | T | |
</math> | </math> | ||
| - | + | es suficiente con especificar | |
| + | <center> | ||
<math> | <math> | ||
| - | x | + | \mathrm{f} \left( \, x \, \right), \, |
| + | \forall x \in \left[ \, a, \, a + T \, \right) | ||
</math> | </math> | ||
| - | + | </center> | |
| + | para cualquier | ||
<math> | <math> | ||
| - | \ | + | a \in \mathbb{R} |
</math> | </math> | ||
| + | . | ||
<br/> | <br/> | ||
| - | + | Si | |
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | es una funcion periodica de periodo | ||
<math> | <math> | ||
T | T | ||
</math> | </math> | ||
| - | | + | , entonces |
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) \, = \, \mathrm{f} \left( \, x \, + \, n \cdot T \, \right) | ||
| + | </math> | ||
| + | para todo numero real | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | y cualquier numero entero | ||
| + | <math> | ||
| + | n | ||
| + | </math>. | ||
<br/> | <br/> | ||
| Línea 67: | Línea 123: | ||
</math> | </math> | ||
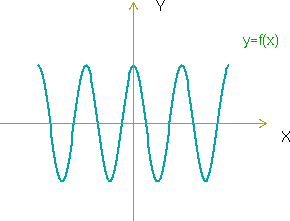
| - | < | + | En este ejemplo, el periodo es |
| + | <math> | ||
| + | \frac{2 \pi}{5} | ||
| + | </math> | ||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
[[Imagen:coseno.png]] | [[Imagen:coseno.png]] | ||
</center> | </center> | ||
| - | |||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
| - | |||
| - | |||
Revisión de 21:49 26 jul 2010
Se dice que una función
 es periódica, de periodo
es periódica, de periodo
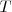 , con
, con
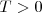 , si y solo si verifica las siguientes dos condiciones:
, si y solo si verifica las siguientes dos condiciones:
1.
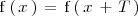 para todo número real
para todo número real
 .
.
2.
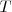 es el menor número positivo que cumple la anterior condición.
es el menor número positivo que cumple la anterior condición.
Tipicas funciones periodicas son las funciones trigonometricas: el coseno, el seno y la tangente.
Son funciones periodicas
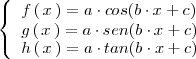
donde
 ,
,
 y
y
 son numeros reales cualesquiera.
son numeros reales cualesquiera.
Una funci\'on constante es una funci\'on periodica.
Para determinar completamente una funci\'on periodica de periodo
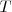 es suficiente con especificar
es suficiente con especificar
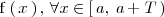
para cualquier
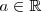 .
.
Si
 es una funcion periodica de periodo
es una funcion periodica de periodo
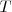 , entonces
, entonces
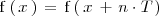 para todo numero real
para todo numero real
 y cualquier numero entero
y cualquier numero entero
 .
.
Ejemplo
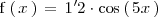
En este ejemplo, el periodo es