¿Qué es una matriz?
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | ==Definición de matriz y tipos de matrices== | ||
| + | |||
| + | <br/> | ||
| + | |||
Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension | Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension | ||
| | ||
| Línea 118: | Línea 122: | ||
| | ||
| - | * la diagonal secundaria formada por los elementos de la forma | + | *la diagonal secundaria formada por los elementos de la forma |
<math> | <math> | ||
a_{ij} | a_{ij} | ||
| Línea 164: | Línea 168: | ||
<br/> | <br/> | ||
| + | |||
| + | Una matriz rectangular es aquella que tiene distinto número de filas que de columnas | ||
| + | | ||
| + | <math> | ||
| + | \left( | ||
| + | m \neq n | ||
| + | \right) | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 1 & -1 & ~~0 | ||
| + | \\ | ||
| + | 2 & ~~3 & -1 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Matriz fila es toda matriz rectangular con una sola fila de dimension | ||
| + | <math> | ||
| + | 1 \times n | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | -1 & 3 & 5 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Matriz columna es toda matriz rectangular con una sola columna de dimension | ||
| + | <math> | ||
| + | m \times 1 | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{c} | ||
| + | -1 | ||
| + | \\ | ||
| + | ~~3 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una matriz nula es una matriz rectangular con todos sus elementos nulos. Se denota por | ||
| + | | ||
| + | <math> | ||
| + | 0 | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Matriz triangular superior es toda matriz cuadrada en la que todos los terminos | ||
| + | situados por debajo de la diagonal principal son ceros | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 1 & -1 & ~~0 | ||
| + | \\ | ||
| + | 0 & ~~3 & -1 | ||
| + | \\ | ||
| + | 0 & ~~0 & ~~2 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Matriz triangular inferior es toda matriz cuadrada en la que todos los terminos | ||
| + | situados por encima de la diagonal principal son ceros | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 2 & ~~0 & 0 | ||
| + | \\ | ||
| + | 3 & -1 & 0 | ||
| + | \\ | ||
| + | 1 & -1 & 3 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Matriz diagonal es toda matriz cuadrada en la que todos los terminos | ||
| + | no situados en la diagonal principal son ceros. | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | ~~2 & ~~0 & ~~0 | ||
| + | \\ | ||
| + | ~~0 & -1 & ~~0 | ||
| + | \\ | ||
| + | ~~0 & ~~0 & ~~3 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Matriz escalar es toda matriz diagonal en la que todos los terminos | ||
| + | de la diagonal principal son iguales. | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 2 & {0} & {0} | ||
| + | \\ | ||
| + | {0} & 2 & {0} | ||
| + | \\ | ||
| + | {0} & {0} & 2 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Matriz unidad es la matriz escalar cuyos elementos de la diagonal principal son todos | ||
| + | | ||
| + | <math> | ||
| + | 1 | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 1 & {0} & {0} | ||
| + | \\ | ||
| + | {0} & 1 & {0} | ||
| + | \\ | ||
| + | {0} & {0} & 1 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Operaciones con matrices== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Dos matrices son iguales si tienen la misma dimension y si los elementos que ocupan el | ||
| + | mismo lugar en ambas, son iguales. | ||
| + | |||
| + | Para dos matrices | ||
| + | <math> | ||
| + | A = \left( a_{ij} \right) | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | B = \left( b_{ij} \right) | ||
| + | </math> | ||
| + | de la misma dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | , la suma de | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | B | ||
| + | </math> | ||
| + | es la matriz de la misma dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | , dada por | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + B = \left( a_{ij} \right) + \left( b_{ij} \right) = \left( a_{ij} + b_{ij} \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A + B = | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | a_{11 }& a_{12} & a_{13} | ||
| + | \\ | ||
| + | a_{21 }& a_{22} & a_{23} | ||
| + | \\ | ||
| + | a_{31 }& a_{32} & a_{33} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | + | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | b_{11 }& b_{12} & b_{13} | ||
| + | \\ | ||
| + | b_{21 }& b_{22} & b_{23} | ||
| + | \\ | ||
| + | b_{31 }& b_{32} & b_{33} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13} | ||
| + | \\ | ||
| + | a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23} | ||
| + | \\ | ||
| + | a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para un número real | ||
| + | <math> | ||
| + | k | ||
| + | </math> | ||
| + | y una matriz | ||
| + | <math> | ||
| + | A = \left( a_{ij} \right)} | ||
| + | </math> | ||
| + | de dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | , el producto de un número real por una matriz es la matriz de la misma dimension | ||
| + | | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | dada por | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | k \cdot A = k \cdot \left( a_{ij} \right) = \left( k \cdot a_{ij} \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Es decir, el producto | ||
| + | <math> | ||
| + | k \cdot A | ||
| + | </math> | ||
| + | se obtiene multiplicando el numero real por cada uno de los elementos de la | ||
| + | matriz. | ||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | k \cdot A = k \cdot | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | a_{11 }& a_{12} | ||
| + | \\ | ||
| + | a_{21 }& a_{22} | ||
| + | \\ | ||
| + | a_{31 }& a_{32} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | k \cdot a_{11 }& k \cdot a_{12} | ||
| + | \\ | ||
| + | k \cdot a_{21 }& k \cdot a_{22} | ||
| + | \\ | ||
| + | k \cdot a_{31 }& k \cdot a_{32} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Producto de matrices== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El producto de dos matrices | ||
| + | <math> | ||
| + | A = \left( a_{ij} \right) | ||
| + | </math> | ||
| + | de dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | B = \left( b_{ij} \right) | ||
| + | </math> | ||
| + | de dimension | ||
| + | <math> | ||
| + | n \times p | ||
| + | </math> | ||
| + | , es la matriz | ||
| + | <math> | ||
| + | A \cdot B | ||
| + | </math> | ||
| + | dada por: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot B = \left( c_{ij} \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | con | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | c_{ij} = \sum_{j = 1}^n a_{ij} \cdot b_{jk} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Es decir, cada elemento | ||
| + | <math> | ||
| + | c_{ik} | ||
| + | </math> | ||
| + | se obtiene multiplicando la fila i-ésima de la primera matriz por la columna | ||
| + | k-ésima de la segunda matriz. | ||
| + | |||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 1 & 2 & 3 | ||
| + | \\ | ||
| + | 4 & 5 & 6 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | \cdot | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | ~~7 & ~~8 | ||
| + | \\ | ||
| + | ~~9 & ~~0 | ||
| + | \\ | ||
| + | -1 & -2 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right) | ||
| + | \\ | ||
| + | 4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right) | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Propiedades:=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | *El producto de matrices cuadradas es asociativo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot | ||
| + | \left( | ||
| + | B \cdot C | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | A \cdot B | ||
| + | \right) | ||
| + | \cdot C | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | *El producto de matrices cuadradas de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | posee como elemento neutro la matriz unidad o identidad | ||
| + | <math> | ||
| + | I | ||
| + | </math> | ||
| + | de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | ya que: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot I = I \cdot A = A | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | * El producto de matrices cuadradas es distributivo respecto de la suma de matrices: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot | ||
| + | \left( | ||
| + | B + C | ||
| + | \right) | ||
| + | = A \cdot B + A \cdot C | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Transposicion de matrices. Matriz simetrica y antisimetrica== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Se llama matriz traspuesta de una matriz | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | de dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | , a la matriz que se obtiene al cambiar en | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | las filas por columnas o las columnas por filas. Se representa por | ||
| + | <math> | ||
| + | A^t | ||
| + | </math> | ||
| + | y su dimension es | ||
| + | <math> | ||
| + | n \times m | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Propiedades:=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | * <math> | ||
| + | \left( \, A^t \, \right)^t = A | ||
| + | </math> | ||
| + | |||
| + | * <math> | ||
| + | \left( \, A + B \, \right)^t = A^t + B^t | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | * <math> | ||
| + | \left( \, k \cdot A \, \right)^t = k \cdot A^t | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | * <math> | ||
| + | \left( \, A \cdot B \, \right)^t = B^t \cdot A^t | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Se llama matriz simetrica a toda matriz cuadrada | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | que coincide con su transpuesta: | ||
| + | <math> | ||
| + | A = A^t | ||
| + | </math>. | ||
| + | En una matriz simetrica cualquier par de elementos simetricos respecto a la | ||
| + | diagonal principal son iguales. | ||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | 1 & 2 & 3 | ||
| + | \\ | ||
| + | 2 & 4 & 5 | ||
| + | \\ | ||
| + | 3 & 5 & 7 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Se llama matriz antisimetrica a toda matriz cuadrada | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | que coincide con la opuesta de su transpuesta: | ||
| + | <math> | ||
| + | A = -A^t | ||
| + | </math>. | ||
| + | En una matriz simetrica cualquier par de elementos simetricos respecto a la | ||
| + | diagonal principal son opuestos. | ||
| + | Ejemplo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{ccc} | ||
| + | ~~ 0 & ~~2 & -3 | ||
| + | \\ | ||
| + | -2 & ~~0 & ~~5 | ||
| + | \\ | ||
| + | ~~ 3 & -5 & ~~0 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Matriz inversa== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La matriz inversa de una matriz cuadrada | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | de orden | ||
| + | <math> | ||
| + | n, | ||
| + | </math> | ||
| + | es la matriz | ||
| + | <math> | ||
| + | , A^{-1}, | ||
| + | </math> | ||
| + | de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | que verifica: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot A^{-1} = A^{-1} \cdot A = I | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices | ||
| + | singulares. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Calculo de la matriz inversa=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para calcular la matriz inversa de una matriz regular podemos utilizar dos | ||
| + | procedimientos: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ====Mediante la definicion==== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Por ejemplo para hallar la matriz inversa de la matriz | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 3 & 7 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | hacemos | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A^{-1} = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | a & b | ||
| + | \\ | ||
| + | c & d | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | como | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | I = A \cdot A^{-1} \Rightarrow | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 3 & 7 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | \cdot | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | a & b | ||
| + | \\ | ||
| + | c & d | ||
| + | \end{array} | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 0 | ||
| + | \\ | ||
| + | 0 & 1 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Operando: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | a + 2c & b + 2d | ||
| + | \\ | ||
| + | 3a + 7c & 3b + 7d | ||
| + | \end{array} | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 0 | ||
| + | \\ | ||
| + | 0 & 1 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | \Leftrightarrow | ||
| + | \left\{ | ||
| + | \begin{array}[c]{ccc} | ||
| + | a + 2c & = & 1 | ||
| + | \\ | ||
| + | 3a + 7c & = & 0 | ||
| + | \\ | ||
| + | b + 2d & = & 0 | ||
| + | \\ | ||
| + | 3b + 7d & = & 1 | ||
| + | \\ | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \Rightarrow \left\{ | ||
| + | \begin{array}[c]{ccc} | ||
| + | a & = & 7 | ||
| + | \\ | ||
| + | b & = & -2 | ||
| + | \\ | ||
| + | c & = & -3 | ||
| + | \\ | ||
| + | d & = & 1 | ||
| + | \\ | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ====Método de Gauss-Jordan==== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La inversa de una matriz regular | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | se calcular transformando la matriz | ||
| + | <math> | ||
| + | \left( | ||
| + | \, A \, \left| \, I \, \right. | ||
| + | \right) | ||
| + | </math> | ||
| + | mediante operaciones elementales por filas en la matriz | ||
| + | <math> | ||
| + | \left( | ||
| + | \, I \, \left| \, A^{-1} \, \right. | ||
| + | \right) | ||
| + | </math> | ||
| + | |||
| + | Las operaciones elementales por filas en una matriz son las siguientes: | ||
| + | |||
| + | # Intercambiar las filas | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | j, | ||
| + | </math> | ||
| + | que designaremos por | ||
| + | <math> | ||
| + | F_i \longrightarrow F_j | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | # Multiplicar la fila | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | por el numero | ||
| + | <math> | ||
| + | k \neq 0 | ||
| + | </math> | ||
| + | y sustituirla por el resultado; lo designamos por | ||
| + | <math> | ||
| + | F_i \tau k \cdot F_i | ||
| + | </math> | ||
| + | |||
| + | # Multiplicar la fila | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | por el numero | ||
| + | <math> | ||
| + | k \neq 0 | ||
| + | </math> | ||
| + | y sustituirla por el resultado; lo designamos por | ||
| + | <math> | ||
| + | F_i \tau k \cdot F_i | ||
| + | </math> | ||
| + | |||
| + | # Sumar las filas | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | j, | ||
| + | </math> | ||
| + | , multiplicadas por sendos números, y llevar el resultado a la fila | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | o | ||
| + | <math> | ||
| + | j | ||
| + | </math> | ||
| + | . Lo designamos por | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | o | ||
| + | <math> | ||
| + | F_j \to k \cdot F_i + t \cdot F_j | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Rango de una matriz== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | En la matriz | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \begin{array}[c]{cccc} | ||
| + | a_{11 }& a_{12} & \ldots & a_{1n} | ||
| + | \\ | ||
| + | a_{21 }& a_{22} & \ldots & a_{2n} | ||
| + | \\ | ||
| + | \vdots & \vdots & \ddots & \vdots | ||
| + | \\ | ||
| + | a_{m1 }& a_{m2} & \ldots & a_{mn} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Se dice que las filas | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | F_i, \, F_j, \, F_k, \, \ldots, \, F_t | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, F_i = | ||
| + | \left( | ||
| + | \, a_{i1 }, \, a_{i2}, \, \ldots, \, a_{in} \, | ||
| + | \right) | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | son dependientes si existen números | ||
| + | <math> | ||
| + | \alpha_j, \, \alpha_k, \, \ldots, \, \alpha_t \in R | ||
| + | </math> | ||
| + | tales que | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | F_i = \alpha_j \cdot F_j + \alpha_k \cdot F_k + \, \ldots \, + \alpha_t \cdot F_t | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | En caso contrario, se dice que las filas | ||
| + | <math> | ||
| + | F_i, \, F_j, \, F_k, \, \ldots, \, F_t | ||
| + | </math> | ||
| + | son linealmente independientes. | ||
| + | |||
| + | El '''rango''' de una matriz es el número de filas o de columnas linealmente independientes | ||
| + | que tiene esa matriz. | ||
Revisión de 01:50 28 nov 2006
Tabla de contenidos |
Definición de matriz y tipos de matrices
Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension
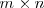 a un conjunto de números reales dispuestos en
a un conjunto de números reales dispuestos en
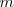 filas y
filas y
 columnas de la siguiente forma
columnas de la siguiente forma
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)](/images/math/math-2b93b39c0505fe91a8bdffdcb317c676.png)
La matriz
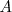 se puede designar tambien como
se puede designar tambien como
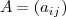 donde
donde
![\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, m
\\
j = 1, \, 2, \, \ldots, \, n
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, m
\\
j = 1, \, 2, \, \ldots, \, n
\end{array}
</pre>
<p>\right.](/images/math/math-22d889e2bbcf6ec56d6db3849ebbe730.png)
Un elemento generico de la matriz se designa por
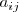 en el cual el subindice
en el cual el subindice
 representa el numero de fila que ocupa el elemento y el subindice
representa el numero de fila que ocupa el elemento y el subindice
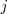 el numero de columna.
el numero de columna.
El conjunto de matrices de dimension
 se denota por:
se denota por:
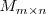
El conjunto de matrices de dimension
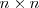 , tambien llamadas de orden
, tambien llamadas de orden
 , se denota por:
, se denota por:
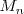
Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:
- la diagonal principal formada por los elementos de la forma
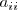
- la diagonal secundaria formada por los elementos de la forma
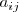 tales que
tales que
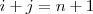
![\begin{array}[c]{cc}
</p>
<pre> \left(
\begin{array}[c]{cccc}
\mathbf{a_{11}} & a_{12} & a_{13} & a_{14}
\\
a_{21} & \mathbf{a_{22}} & a_{23} & a_{24}
\\
a_{31} & a_{32} & \mathbf{a_{33}} & a_{34}
\\
a_{41} & a_{42} & a_{43} & \mathbf{a_{44}}
\end{array}
\right)
&
\left(
\begin{array}[c]{cccc}
a_{11} & a_{12} & a_{13} & \mathbf{a_{14}}
\\
a_{21} & a_{22} & \mathbf{a_{23}} & a_{24}
\\
a_{31} & \mathbf{a_{32}} & a_{33} & a_{34}
\\
\mathbf{a_{41}} & a_{42} & a_{43} & a_{44}
\end{array}
\right)
\\
&
\\
\makebox{Diagonal principal} & \makebox{Diagonal secundaria}
</pre>
<p>\end{array}
\begin{array}[c]{cc}
</p>
<pre> \left(
\begin{array}[c]{cccc}
\mathbf{a_{11}} & a_{12} & a_{13} & a_{14}
\\
a_{21} & \mathbf{a_{22}} & a_{23} & a_{24}
\\
a_{31} & a_{32} & \mathbf{a_{33}} & a_{34}
\\
a_{41} & a_{42} & a_{43} & \mathbf{a_{44}}
\end{array}
\right)
&
\left(
\begin{array}[c]{cccc}
a_{11} & a_{12} & a_{13} & \mathbf{a_{14}}
\\
a_{21} & a_{22} & \mathbf{a_{23}} & a_{24}
\\
a_{31} & \mathbf{a_{32}} & a_{33} & a_{34}
\\
\mathbf{a_{41}} & a_{42} & a_{43} & a_{44}
\end{array}
\right)
\\
&
\\
\makebox{Diagonal principal} & \makebox{Diagonal secundaria}
</pre>
<p>\end{array}](/images/math/math-b55d3ab2d5b012a0fa6f3b9542f554e5.png)
Una matriz rectangular es aquella que tiene distinto número de filas que de columnas
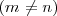
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
2 & ~~3 & -1
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
2 & ~~3 & -1
\end{array}
\right)
</pre>
<p>](/images/math/math-77539f199b63acde3f386891e6643924.png)
Matriz fila es toda matriz rectangular con una sola fila de dimension
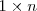
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
-1 & 3 & 5
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
-1 & 3 & 5
\end{array}
\right)
</pre>
<p>](/images/math/math-ddcaa947e9641f093ec0f8d2c0d583d9.png)
Matriz columna es toda matriz rectangular con una sola columna de dimension
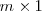
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{c}
-1
\\
~~3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{c}
-1
\\
~~3
\end{array}
\right)
</pre>
<p>](/images/math/math-6e25da3e668f5afabb9e8999290f43de.png)
Una matriz nula es una matriz rectangular con todos sus elementos nulos. Se denota por
 .
.
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
0 & 0 & 0
\\
0 & 0 & 0
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
0 & 0 & 0
\\
0 & 0 & 0
\end{array}
\right)
</pre>
<p>](/images/math/math-5843638a226353656790577733c70017.png)
Matriz triangular superior es toda matriz cuadrada en la que todos los terminos situados por debajo de la diagonal principal son ceros
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
0 & ~~3 & -1
\\
0 & ~~0 & ~~2
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
0 & ~~3 & -1
\\
0 & ~~0 & ~~2
\end{array}
\right)
</pre>
<p>](/images/math/math-bc3f0df47bfb80a397ae4b8f23b8c0aa.png)
Matriz triangular inferior es toda matriz cuadrada en la que todos los terminos situados por encima de la diagonal principal son ceros
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & ~~0 & 0
\\
3 & -1 & 0
\\
1 & -1 & 3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & ~~0 & 0
\\
3 & -1 & 0
\\
1 & -1 & 3
\end{array}
\right)
</pre>
<p>](/images/math/math-82e48a12244d0a664439764d8460b342.png)
Matriz diagonal es toda matriz cuadrada en la que todos los terminos no situados en la diagonal principal son ceros.
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
~~2 & ~~0 & ~~0
\\
~~0 & -1 & ~~0
\\
~~0 & ~~0 & ~~3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
~~2 & ~~0 & ~~0
\\
~~0 & -1 & ~~0
\\
~~0 & ~~0 & ~~3
\end{array}
\right)
</pre>
<p>](/images/math/math-7243130e96bfab5fa81a6d6c3f538afa.png)
Matriz escalar es toda matriz diagonal en la que todos los terminos de la diagonal principal son iguales.
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & {0} & {0}
\\
{0} & 2 & {0}
\\
{0} & {0} & 2
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & {0} & {0}
\\
{0} & 2 & {0}
\\
{0} & {0} & 2
\end{array}
\right)
</pre>
<p>](/images/math/math-0c8108a994f140b623c5323aab03f2e4.png)
Matriz unidad es la matriz escalar cuyos elementos de la diagonal principal son todos
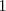 .
.
Ejemplo:
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & {0} & {0}
\\
{0} & 1 & {0}
\\
{0} & {0} & 1
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & {0} & {0}
\\
{0} & 1 & {0}
\\
{0} & {0} & 1
\end{array}
\right)
</pre>
<p>](/images/math/math-992b5c285926278d809ff3bdadf8a15d.png)
Operaciones con matrices
Dos matrices son iguales si tienen la misma dimension y si los elementos que ocupan el mismo lugar en ambas, son iguales.
Para dos matrices
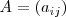 y
y
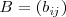 de la misma dimension
de la misma dimension
 , la suma de
, la suma de
 y
y
 es la matriz de la misma dimension
es la matriz de la misma dimension
 , dada por
, dada por
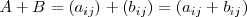
Ejemplo:
![A + B =
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 }& a_{12} & a_{13}
\\
a_{21 }& a_{22} & a_{23}
\\
a_{31 }& a_{32} & a_{33}
\end{array}
</pre>
<p>\right)
+
\left(
</p>
<pre> \begin{array}[c]{ccc}
b_{11 }& b_{12} & b_{13}
\\
b_{21 }& b_{22} & b_{23}
\\
b_{31 }& b_{32} & b_{33}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
\\
a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
\\
a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
\end{array}
</pre>
<p>\right)
A + B =
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 }& a_{12} & a_{13}
\\
a_{21 }& a_{22} & a_{23}
\\
a_{31 }& a_{32} & a_{33}
\end{array}
</pre>
<p>\right)
+
\left(
</p>
<pre> \begin{array}[c]{ccc}
b_{11 }& b_{12} & b_{13}
\\
b_{21 }& b_{22} & b_{23}
\\
b_{31 }& b_{32} & b_{33}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
\\
a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
\\
a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
\end{array}
</pre>
<p>\right)](/images/math/math-83b07e70030828d73f75b5a4cd132a90.png)
Para un número real
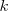 y una matriz
y una matriz
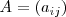 de dimension
de dimension
 , el producto de un número real por una matriz es la matriz de la misma dimension
, el producto de un número real por una matriz es la matriz de la misma dimension
 dada por
dada por
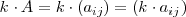
Es decir, el producto
 se obtiene multiplicando el numero real por cada uno de los elementos de la
matriz.
Ejemplo:
se obtiene multiplicando el numero real por cada uno de los elementos de la
matriz.
Ejemplo:
![k \cdot A = k \cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11 }& a_{12}
\\
a_{21 }& a_{22}
\\
a_{31 }& a_{32}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
k \cdot a_{11 }& k \cdot a_{12}
\\
k \cdot a_{21 }& k \cdot a_{22}
\\
k \cdot a_{31 }& k \cdot a_{32}
\end{array}
</pre>
<p>\right)
k \cdot A = k \cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11 }& a_{12}
\\
a_{21 }& a_{22}
\\
a_{31 }& a_{32}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
k \cdot a_{11 }& k \cdot a_{12}
\\
k \cdot a_{21 }& k \cdot a_{22}
\\
k \cdot a_{31 }& k \cdot a_{32}
\end{array}
</pre>
<p>\right)](/images/math/math-ac0775a178d76f16f0d842a39ec92976.png)
Producto de matrices
El producto de dos matrices
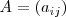 de dimension
de dimension
 y
y
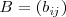 de dimension
de dimension
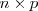 , es la matriz
, es la matriz
 dada por:
dada por:
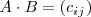
con
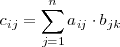
Es decir, cada elemento
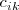 se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
k-ésima de la segunda matriz.
se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
k-ésima de la segunda matriz.
Ejemplo:
![\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
4 & 5 & 6
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
~~7 & ~~8
\\
~~9 & ~~0
\\
-1 & -2
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
\\
4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
4 & 5 & 6
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
~~7 & ~~8
\\
~~9 & ~~0
\\
-1 & -2
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
\\
4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
\end{array}
</pre>
<p>\right)](/images/math/math-2ff8eff26cdd9448d6141d459441e2d9.png)
Propiedades:
- El producto de matrices cuadradas es asociativo:
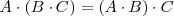
- El producto de matrices cuadradas de orden
 posee como elemento neutro la matriz unidad o identidad
posee como elemento neutro la matriz unidad o identidad
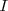 de orden
de orden
 ya que:
ya que:
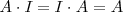
- El producto de matrices cuadradas es distributivo respecto de la suma de matrices:
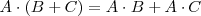
Transposicion de matrices. Matriz simetrica y antisimetrica
Se llama matriz traspuesta de una matriz
 de dimension
de dimension
 , a la matriz que se obtiene al cambiar en
, a la matriz que se obtiene al cambiar en
 las filas por columnas o las columnas por filas. Se representa por
las filas por columnas o las columnas por filas. Se representa por
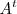 y su dimension es
y su dimension es
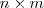
Propiedades:
-
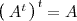
-
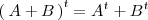
-
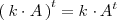
-
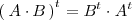
Se llama matriz simetrica a toda matriz cuadrada
 que coincide con su transpuesta:
que coincide con su transpuesta:
 .
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son iguales.
Ejemplo:
.
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son iguales.
Ejemplo:
![\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 4 & 5
\\
3 & 5 & 7
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 4 & 5
\\
3 & 5 & 7
\end{array}
</pre>
<p>\right)](/images/math/math-707d3163e2789bbadd06f90a3c397c08.png)
Se llama matriz antisimetrica a toda matriz cuadrada
 que coincide con la opuesta de su transpuesta:
que coincide con la opuesta de su transpuesta:
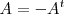 .
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son opuestos.
Ejemplo:
.
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son opuestos.
Ejemplo:
![\left(
</p>
<pre> \begin{array}[c]{ccc}
~~ 0 & ~~2 & -3
\\
-2 & ~~0 & ~~5
\\
~~ 3 & -5 & ~~0
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
~~ 0 & ~~2 & -3
\\
-2 & ~~0 & ~~5
\\
~~ 3 & -5 & ~~0
\end{array}
</pre>
<p>\right)](/images/math/math-790d68307dd50a5291399ef733c5b199.png)
Matriz inversa
La matriz inversa de una matriz cuadrada
 de orden
de orden
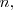 es la matriz
es la matriz
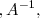 de orden
de orden
 que verifica:
que verifica:
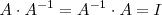
Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices singulares.
Calculo de la matriz inversa
Para calcular la matriz inversa de una matriz regular podemos utilizar dos procedimientos:
Mediante la definicion
Por ejemplo para hallar la matriz inversa de la matriz
![A =
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
A =
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)](/images/math/math-1fe0b90602bd956d6622d417fadb9a6d.png)
hacemos
![A^{-1} =
\left(
</p>
<pre> \begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
A^{-1} =
\left(
</p>
<pre> \begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)](/images/math/math-86eccf1851904f21df88d4e8caf4391c.png)
como
![I = A \cdot A^{-1} \Rightarrow
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
I = A \cdot A^{-1} \Rightarrow
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)](/images/math/math-83c4208e822a9057faf4bc22eb75b114.png)
Operando:
![\left(
</p>
<pre> \begin{array}[c]{cc}
a + 2c & b + 2d
\\
3a + 7c & 3b + 7d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
\Leftrightarrow
\left\{
</p>
<pre> \begin{array}[c]{ccc}
a + 2c & = & 1
\\
3a + 7c & = & 0
\\
b + 2d & = & 0
\\
3b + 7d & = & 1
\\
\end{array}
</pre>
<p>\right.
\left(
</p>
<pre> \begin{array}[c]{cc}
a + 2c & b + 2d
\\
3a + 7c & 3b + 7d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
\Leftrightarrow
\left\{
</p>
<pre> \begin{array}[c]{ccc}
a + 2c & = & 1
\\
3a + 7c & = & 0
\\
b + 2d & = & 0
\\
3b + 7d & = & 1
\\
\end{array}
</pre>
<p>\right.](/images/math/math-65ac35f7477a5f157f8f4b5954474b3d.png)
![\Rightarrow \left\{
</p>
<pre> \begin{array}[c]{ccc}
a & = & 7
\\
b & = & -2
\\
c & = & -3
\\
d & = & 1
\\
\end{array}
</pre>
<p>\right.
\Rightarrow \left\{
</p>
<pre> \begin{array}[c]{ccc}
a & = & 7
\\
b & = & -2
\\
c & = & -3
\\
d & = & 1
\\
\end{array}
</pre>
<p>\right.](/images/math/math-d80915bcc5f5cebafc112b3692daef76.png)
Método de Gauss-Jordan
La inversa de una matriz regular
 se calcular transformando la matriz
se calcular transformando la matriz
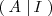 mediante operaciones elementales por filas en la matriz
mediante operaciones elementales por filas en la matriz
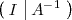
Las operaciones elementales por filas en una matriz son las siguientes:
- Intercambiar las filas
 y
y
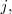 que designaremos por
que designaremos por

- Multiplicar la fila
 por el numero
por el numero
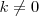 y sustituirla por el resultado; lo designamos por
y sustituirla por el resultado; lo designamos por
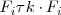
- Multiplicar la fila
 por el numero
por el numero
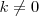 y sustituirla por el resultado; lo designamos por
y sustituirla por el resultado; lo designamos por
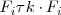
- Sumar las filas
 y
y
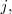 , multiplicadas por sendos números, y llevar el resultado a la fila
, multiplicadas por sendos números, y llevar el resultado a la fila
 o
o
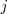 . Lo designamos por
. Lo designamos por
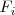 o
o
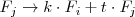
Rango de una matriz
En la matriz
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)](/images/math/math-2b93b39c0505fe91a8bdffdcb317c676.png)
Se dice que las filas
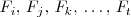
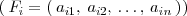
son dependientes si existen números
 tales que
tales que
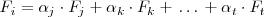
En caso contrario, se dice que las filas
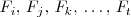 son linealmente independientes.
son linealmente independientes.
El rango de una matriz es el número de filas o de columnas linealmente independientes que tiene esa matriz.
Tweet
-
-
-



