Métodos de resolución de sistemas de ecuaciones lineales
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | + | __TOC__ | |
| - | + | ==Definición== | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | La matriz inversa de una [[¿Qué es una matriz?#Matrices cuadradas|matriz cuadrada]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | \mathbf{A} | |
</math> | </math> | ||
| - | + | de orden | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | n, | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | es la matriz cuadrada | |
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \ | + | \mathbf{A}^{-1} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | tambien de orden | |
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | n | |
</math> | </math> | ||
| - | + | que verifica: | |
| - | que | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
| - | |||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \mathbf{A} \cdot \mathbf{A}^{-1} = \mathbf{A}^{-1} \cdot \mathbf{A} = I | |
</math> | </math> | ||
</center> | </center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
<br/> | <br/> | ||
| - | + | donde | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \ | + | \mathbf{I} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | es la | |
| - | + | [[¿Qué es una matriz?#Matrices unidad o identidad|matriz identidad]] de orden | |
<math> | <math> | ||
| - | + | n | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | . | |
| - | + | ||
<br/> | <br/> | ||
| - | + | ==Exitencia de la matriz inversa== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Las matrices que tienen inversa se llaman '''''regulares''''' y las que NO | |
| - | + | tienen inversa, '''''singulares'''''. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | . | + | |
<br/> | <br/> | ||
| - | Una | + | Una matriz cuadrada de orden n es regular si, y solo si, su [[Rango de una matriz|rango]] es n. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Una matriz cuadrada de orden n es singular si, y solo si, su [[Definición de determinante|determinante]] es cero. | |
<br/> | <br/> | ||
| - | + | ==Propiedades== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Las propiedades más importantes relativas a la matriz inversa son las siguientes: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | 1. Si existe, | |
| - | <math> | + | <math> |
| - | + | \mathbf{A}^{-1} | |
</math> | </math> | ||
| - | + | es única. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | 2. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \left | + | \left( |
| - | \ | + | \mathbf{A}^{-1} |
| - | + | \right) | |
| - | + | ^{-1} = \mathbf{A} | |
| - | + | ||
| - | \ | + | |
| - | + | ||
</math> | </math> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<br/> | <br/> | ||
| - | + | 3. | |
<math> | <math> | ||
| - | + | \left( | |
| - | + | \mathbf{A} \cdot \mathbf{B} | |
| - | + | \right) | |
| - | + | ^{-1} = \mathbf{B}^{-1} \cdot \mathbf{A}^{-1} | |
| - | + | ||
</math> | </math> | ||
| - | |||
<br/> | <br/> | ||
| - | + | 4. El determinante de una matriz regular | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | \ | + | \mathbf{A} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | + | es el inverso del determinante de su matriz inversa: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left| \mathbf{A}^{-1} \right| = \frac{1}{\left| \mathbf{A} \right|} | |
</math> | </math> | ||
</center> | </center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
<br/> | <br/> | ||
| - | == | + | ==Cálculo de la matriz inversa== |
<br/> | <br/> | ||
| - | + | La matriz inversa de una matriz regular se puede calcular de diferentes maneras: | |
| - | + | ||
<br/> | <br/> | ||
| - | + | ===Resolviendo un sistema de ecuaciones lineales=== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | de | + | |
<br/> | <br/> | ||
| - | + | ====Ejemplo==== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | = | + | <center> |
| + | <math> | ||
| + | \mathbf{A} = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 3 & 7 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | hacemos | |
<br/> | <br/> | ||
| Línea 437: | Línea 152: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \mathbf{A}^{-1} = |
| - | + | \left( | |
| - | + | \begin{array}[c]{cc} | |
| - | + | a & b | |
| - | + | \\ | |
| - | + | c & d | |
| - | + | \end{array} | |
| - | + | \right) | |
| - | \right | + | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 451: | Línea 165: | ||
<br/> | <br/> | ||
| - | + | como | |
<br/> | <br/> | ||
| Línea 457: | Línea 171: | ||
<center> | <center> | ||
<math> | <math> | ||
| + | I = \mathbf{A} \cdot \mathbf{A}^{-1} \Rightarrow | ||
\left( | \left( | ||
| - | + | \begin{array}[c]{cc} | |
| - | + | 1 & 2 | |
| - | + | \\ | |
| - | + | 3 & 7 | |
| - | + | \end{array} | |
| - | + | \right) | |
| - | + | \cdot | |
| - | + | \left( | |
| - | + | \begin{array}[c]{cc} | |
| - | + | a & b | |
| - | + | \\ | |
| - | + | c & d | |
| - | + | \end{array} | |
| - | + | \right) | |
| - | + | = | |
| - | + | \left( | |
| + | \begin{array}[c]{cc} | ||
| + | 1 & 0 | ||
| + | \\ | ||
| + | 0 & 1 | ||
| + | \end{array} | ||
\right) | \right) | ||
</math> | </math> | ||
| Línea 480: | Línea 200: | ||
<br/> | <br/> | ||
| - | + | Operando: | |
<br/> | <br/> | ||
| Línea 487: | Línea 207: | ||
<math> | <math> | ||
\left( | \left( | ||
| - | + | \begin{array}[c]{cc} | |
| - | + | a + 2c & b + 2d | |
| - | + | \\ | |
| - | + | 3a + 7c & 3b + 7d | |
| - | + | \end{array} | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
\right) | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 0 | ||
| + | \\ | ||
| + | 0 & 1 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | \Leftrightarrow | ||
| + | \left\{ | ||
| + | \begin{array}[c]{ccc} | ||
| + | a + 2c & = & 1 | ||
| + | \\ | ||
| + | 3a + 7c & = & 0 | ||
| + | \\ | ||
| + | b + 2d & = & 0 | ||
| + | \\ | ||
| + | 3b + 7d & = & 1 | ||
| + | \\ | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 509: | Línea 239: | ||
<br/> | <br/> | ||
| - | + | <center> | |
| - | + | <math> | |
| + | \Rightarrow \left\{ | ||
| + | \begin{array}[c]{ccc} | ||
| + | a & = & 7 | ||
| + | \\ | ||
| + | b & = & -2 | ||
| + | \\ | ||
| + | c & = & -3 | ||
| + | \\ | ||
| + | d & = & 1 | ||
| + | \\ | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | ===Por el método de Gauss=== | |
<br/> | <br/> | ||
| - | < | + | La inversa de una matriz regular |
| + | <math> | ||
| + | \mathbf{A} | ||
| + | </math> | ||
| + | se puede calcular transformando la matriz | ||
<math> | <math> | ||
\left( | \left( | ||
| - | + | \, \mathbf{A} \, \left| \, \mathbf{I} \, \right. | |
| - | + | \right) | |
| - | + | </math> | |
| - | + | mediante operaciones elementales con las filas de la matriz | |
| - | + | <math> | |
| - | + | \left( | |
| - | + | \, \mathbf{I} \, \left| \, \mathbf{A}^{-1} \, \right. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
\right) | \right) | ||
</math> | </math> | ||
| - | |||
<br/> | <br/> | ||
| - | + | ====Operaciones elementales con las filas de una matriz==== | |
<br/> | <br/> | ||
| - | + | Las operaciones elementales con las filas de una matriz que podemos realizar en | |
| - | + | el metodo de Gauss son las siguientes: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | 1. Intercambiar las filas | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | F_i | |
</math> | </math> | ||
| - | | + | y |
| + | <math> | ||
| + | F_j | ||
| + | </math>. | ||
| + | Esta operación la representaremos así | ||
<br/> | <br/> | ||
| Línea 577: | Línea 304: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | F_i \longleftrightarrow F_j | |
</math> | </math> | ||
</center> | </center> | ||
<br/> | <br/> | ||
| - | + | ||
| + | 2. Multiplicar la fila | ||
<math> | <math> | ||
| - | + | F_i | |
</math> | </math> | ||
| - | por | + | por el número |
<math> | <math> | ||
| - | + | s \neq 0 | |
</math> | </math> | ||
| - | | + | y sustituir |
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | por | ||
| + | <math> | ||
| + | s \cdot F_i | ||
| + | </math>. | ||
| + | Esta operación la representamos de la | ||
| + | siguiente forma: | ||
<br/> | <br/> | ||
| Línea 596: | Línea 333: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | s \cdot F_i \longrightarrow F_i |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 608: | Línea 339: | ||
<br/> | <br/> | ||
| - | + | 3. Sumar las filas | |
<math> | <math> | ||
| - | + | F_i | |
</math> | </math> | ||
| - | + | y | |
<math> | <math> | ||
| - | + | F_j | |
| + | </math>, | ||
| + | multiplicadas por sendos números, | ||
| + | <math> | ||
| + | s | ||
</math> | </math> | ||
| - | |||
| - | |||
y | y | ||
| - | |||
| - | |||
<math> | <math> | ||
| - | + | t | |
| - | </math> | + | </math>, |
| - | + | y sustituir | |
<math> | <math> | ||
| - | + | F_i | |
</math> | </math> | ||
| - | : | + | por el resultado de esta suma. Lo representamos así: |
<br/> | <br/> | ||
| Línea 634: | Línea 365: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | s \cdot F_i + t \cdot F_j \longrightarrow F_i | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 640: | Línea 371: | ||
<br/> | <br/> | ||
| - | que | + | Notese que el segundo tipo de operación, |
| + | <math> | ||
| + | s \cdot F_i \longrightarrow F_i | ||
| + | </math>, | ||
| + | | ||
| + | es un caso particular de esta última propiedad que se tiene cuando | ||
| + | <math> | ||
| + | t = 0 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | ===Mediante la matriz adjunta=== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | La matriz inversa de una matriz regular | |
| - | + | <math> | |
| - | + | \mathbf{A} | |
| + | </math> | ||
| + | se puede calcular mediante la expresión: | ||
<br/> | <br/> | ||
<center> | <center> | ||
| - | <math> | + | <math> |
| - | \mathbf{A} \ | + | \mathbf{A}^{-1} = \frac{1}{\left| \mathbf{A} \right|} \cdot |
| - | </math> | + | \left[ |
| - | </center> | + | \makebox{Adj} |
| + | \left( | ||
| + | \, \mathbf{A} \, | ||
| + | \right) | ||
| + | \right] | ||
| + | ^t | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | donde | |
<math> | <math> | ||
| - | \mathbf{A} | + | \makebox{Adj} |
| + | \left( | ||
| + | \, \mathbf{A} \, | ||
| + | \right) | ||
</math> | </math> | ||
| - | | + | es la [[Matriz inversa#Mediante la matriz adjunta| matriz adjunta]] de |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
| - | </math> | + | </math>. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | ====Definición de matriz adjunta==== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | La matriz cuyos elementos son los correspondientes [[Desarrollo de un determinante#Menores complementarios y adjuntos|adjuntos]] de los elementos de una matriz cuadrada | |
| + | | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | | + | se llama '''''matriz adjunta''''' de |
<math> | <math> | ||
| - | \mathbf{ | + | \mathbf{A} |
</math> | </math> | ||
| - | + | y se denota por | |
| - | + | <math> | |
| - | < | + | \makebox{Adj} \left( \mathbf{A} \right) |
| - | + | </math>. | |
| - | + | El elemento en la i-esima fila y j-esima columna de la matriz adjunta de | |
| - | + | ||
| - | < | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | | + | es |
| + | <math> | ||
| + | A_{ij} | ||
| + | </math>, | ||
| + | el adjunto del elemento de | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | en su fila i-esima y columna j-esima | |
| - | + | <math> | |
| + | \left( \, a_{ij} \, \right)} | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | ====Ejemplo==== | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Los [[Desarrollo de un determinante#Menores complementarios y adjuntos|menores | ||
| + | complementarios]] de los elementos de la matriz | ||
<br/> | <br/> | ||
| Línea 732: | Línea 471: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \left | + | \mathbf{A} = |
| - | \begin{array}{ | + | \left( |
| - | + | \begin{array}{ccc} | |
| + | 1 & 2 & 3 | ||
\\ | \\ | ||
| - | + | 4 & 5 & 6 | |
\\ | \\ | ||
| - | + | 7 & 8 & 0 | |
| - | + | ||
| - | + | ||
\end{array} | \end{array} | ||
| - | \right | + | \right) |
</math> | </math> | ||
</center> | </center> | ||
| Línea 748: | Línea 486: | ||
<br/> | <br/> | ||
| - | + | son | |
<br/> | <br/> | ||
| Línea 754: | Línea 492: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \begin{array}{ccc} | |
| - | { | + | \alpha_{11} = |
| - | + | \left| | |
| - | + | \begin{array}[c]{cc} | |
| - | + | 5 & 6 | |
| - | + | \\ | |
| - | + | 8 & 0 | |
| - | + | \end{array} | |
| - | + | \right| | |
| - | + | & | |
| - | + | \qquad \alpha_{12} = | |
| - | \end{array} | + | \left| |
| - | + | \begin{array}[c]{cc} | |
| - | + | 4 & 6 | |
| - | + | \\ | |
| - | + | 7 & 0 | |
| - | + | \end{array} | |
| - | + | \right| | |
| - | + | & | |
| - | + | \qquad \alpha_{13} = | |
| - | + | \left| | |
| - | + | \begin{array}[c]{cc} | |
| - | + | 4 & 5 | |
| - | + | \\ | |
| - | + | 7 & 8 | |
| - | + | \end{array} | |
| - | + | \right| | |
| - | + | \end{array} | |
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| - | |||
| - | |||
| - | |||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \begin{array}{ccc} |
| - | { | + | \alpha_{21} = |
| - | + | \left| | |
| - | + | \begin{array}[c]{cc} | |
| - | + | 2 & 3 | |
| - | + | \\ | |
| - | + | 8 & 0 | |
| - | + | \end{array} | |
| - | + | \right| | |
| - | + | & | |
| - | + | \qquad \alpha_{22} = | |
| - | \end{array} | + | \left| |
| - | + | \begin{array}[c]{cc} | |
| - | + | 1 & 3 | |
| - | {|\ | + | \\ |
| - | \ | + | 7 & 0 |
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{23} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 7 & 8 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{ccc} | ||
| + | \alpha_{31} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 2 & 3 | ||
| + | \\ | ||
| + | 5 & 6 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{32} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 3 | ||
| + | \\ | ||
| + | 4 & 6 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{33} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 4 & 5 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 812: | Línea 589: | ||
<br/> | <br/> | ||
| - | + | Los adjuntos de los elementos de | |
| + | <math> | ||
| + | \mathbf{A} | ||
| + | </math> | ||
| + | son: | ||
<br/> | <br/> | ||
| Línea 818: | Línea 599: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \begin{array}{ccccccccccc} | |
| + | A_{11} & = & -48 & \qquad & A_{12} & = & ~42 & \qquad & A_{13} & = & -3 | ||
| + | \\ | ||
| + | A_{21} & = & ~24 & \qquad & A_{22} & = & -21 & \qquad & A_{23} & = & ~6 | ||
| + | \\ | ||
| + | A_{31} & = & ~-3 & \qquad & A_{32} & = & ~~6 & \qquad & A_{33} & = & -3 | ||
| + | &\end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 824: | Línea 611: | ||
<br/> | <br/> | ||
| - | + | La matriz adjunta de | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | | + | es |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| Línea 849: | Línea 621: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \left\{ | + | \makebox{Adj} \left( \mathbf{A} \right) = |
| - | \begin{array} | + | \left( |
| - | + | \begin{array}{ccc} | |
| - | + | -48 & ~42 & -3 | |
| - | + | \\ | |
| - | + | ~24 & -21 & ~6 | |
| - | \right | + | \\ |
| + | ~-3 & ~~6 & -3 | ||
| + | \end{array} | ||
| + | \right) | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 861: | Línea 636: | ||
<br/> | <br/> | ||
| - | + | El determinante de | |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | lo podemos calcular [[Desarrollo de un determinante#Desarrollo de un determinante|desarrollando]] por la primera fila: | |
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
| - | |\mathbf{A} | + | \left| \mathbf{A} \right| = a_{11} \cdot A_{11} + a_{12} \cdot A_{12} + a_{13} |
| - | + | \cdot A_{13} = 1 \cdot \left( \, -48 \, \right) + 2 \cdot 42 + 3 \cdot \left( \, | |
| - | + | -3 \, \right) = 25 | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | \right | + | |
| - | \ | + | |
</math> | </math> | ||
| - | + | </center> | |
<br/> | <br/> | ||
| + | Por lo tanto, la matriz inversa de | ||
| + | <math> | ||
| + | \mathbf{A} | ||
| + | </math> | ||
| + | es | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \mathbf{A}^{-1} = \frac{1}{\left| \mathbf{A} \right|} \cdot | |
| - | { | + | \left[ |
| - | + | \makebox{Adj} | |
| - | + | \left( | |
| - | + | \, \mathbf{A} \, | |
| - | + | \right) | |
| - | + | \right] | |
| - | + | ^t = | |
| - | \ | + | \frac{1}{25} \cdot |
| - | + | \left( | |
| - | + | \begin{array}{ccc} | |
| - | \ | + | -48 & ~24 & -3 |
| - | + | \\ | |
| - | + | ~42 & -21 & ~6 | |
| - | + | \\ | |
| - | + | ~-3 & ~~6 & -3 | |
| - | + | \end{array} | |
| - | + | \right) | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| - | <br | + | ==Ejercicios resueltos== |
| + | |||
| + | <br> | ||
| + | |||
| + | [http://www.educared.net/universidad/asp_problemas/problemasvisualizar.asp?idAsignatura=1&idProblema=46 Producto e invertibilidad de matrices] | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 09:15 9 oct 2010
Tabla de contenidos[ocultar] |
Definición
La matriz inversa de una matriz cuadrada
 de orden
de orden
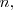 es la matriz cuadrada
es la matriz cuadrada
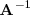 tambien de orden
tambien de orden
 que verifica:
que verifica:
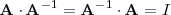
donde
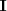 es la
matriz identidad de orden
es la
matriz identidad de orden
 .
.
Exitencia de la matriz inversa
Las matrices que tienen inversa se llaman regulares y las que NO tienen inversa, singulares.
Una matriz cuadrada de orden n es regular si, y solo si, su rango es n.
Una matriz cuadrada de orden n es singular si, y solo si, su determinante es cero.
Propiedades
Las propiedades más importantes relativas a la matriz inversa son las siguientes:
1. Si existe,
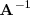 es única.
es única.
2.
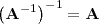
3.
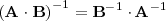
4. El determinante de una matriz regular
 es el inverso del determinante de su matriz inversa:
es el inverso del determinante de su matriz inversa:
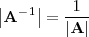
Cálculo de la matriz inversa
La matriz inversa de una matriz regular se puede calcular de diferentes maneras:
Resolviendo un sistema de ecuaciones lineales
Ejemplo
![\mathbf{A} =
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\mathbf{A} =
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)](/images/math/math-d3c460d516d831322ba7600ca96f6a29.png)
hacemos
![\mathbf{A}^{-1} =
\left(
</p>
<pre>\begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
\mathbf{A}^{-1} =
\left(
</p>
<pre>\begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)](/images/math/math-b12d162319feb566da12a07314221b42.png)
como
![I = \mathbf{A} \cdot \mathbf{A}^{-1} \Rightarrow
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre>\begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
I = \mathbf{A} \cdot \mathbf{A}^{-1} \Rightarrow
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre>\begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)](/images/math/math-fa501e8cfad8bd98f052c91797b3f2ac.png)
Operando:
![\left(
</p>
<pre>\begin{array}[c]{cc}
a + 2c & b + 2d
\\
3a + 7c & 3b + 7d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
\Leftrightarrow
\left\{
</p>
<pre>\begin{array}[c]{ccc}
a + 2c & = & 1
\\
3a + 7c & = & 0
\\
b + 2d & = & 0
\\
3b + 7d & = & 1
\\
\end{array}
</pre>
<p>\right.
\left(
</p>
<pre>\begin{array}[c]{cc}
a + 2c & b + 2d
\\
3a + 7c & 3b + 7d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre>\begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
\Leftrightarrow
\left\{
</p>
<pre>\begin{array}[c]{ccc}
a + 2c & = & 1
\\
3a + 7c & = & 0
\\
b + 2d & = & 0
\\
3b + 7d & = & 1
\\
\end{array}
</pre>
<p>\right.](/images/math/math-93a8bef606b968108c4d48ceab054cc5.png)
![\Rightarrow \left\{
</p>
<pre>\begin{array}[c]{ccc}
a & = & 7
\\
b & = & -2
\\
c & = & -3
\\
d & = & 1
\\
\end{array}
</pre>
<p>\right.
\Rightarrow \left\{
</p>
<pre>\begin{array}[c]{ccc}
a & = & 7
\\
b & = & -2
\\
c & = & -3
\\
d & = & 1
\\
\end{array}
</pre>
<p>\right.](/images/math/math-072f3c94488adaa3f7cfe063dd9b30f2.png)
Por el método de Gauss
La inversa de una matriz regular
 se puede calcular transformando la matriz
se puede calcular transformando la matriz
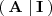 mediante operaciones elementales con las filas de la matriz
mediante operaciones elementales con las filas de la matriz
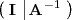
Operaciones elementales con las filas de una matriz
Las operaciones elementales con las filas de una matriz que podemos realizar en el metodo de Gauss son las siguientes:
1. Intercambiar las filas
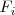 y
y
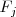 .
Esta operación la representaremos así
.
Esta operación la representaremos así

2. Multiplicar la fila
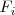 por el número
por el número
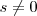 y sustituir
y sustituir
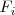 por
por
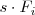 .
Esta operación la representamos de la
siguiente forma:
.
Esta operación la representamos de la
siguiente forma:
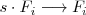
3. Sumar las filas
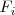 y
y
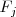 ,
multiplicadas por sendos números,
,
multiplicadas por sendos números,
 y
y
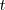 ,
y sustituir
,
y sustituir
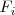 por el resultado de esta suma. Lo representamos así:
por el resultado de esta suma. Lo representamos así:
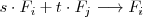
Notese que el segundo tipo de operación,
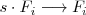 ,
es un caso particular de esta última propiedad que se tiene cuando
,
es un caso particular de esta última propiedad que se tiene cuando
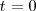 .
.
Mediante la matriz adjunta
La matriz inversa de una matriz regular
 se puede calcular mediante la expresión:
se puede calcular mediante la expresión:
donde
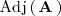 es la matriz adjunta de
es la matriz adjunta de
 .
.
Definición de matriz adjunta
La matriz cuyos elementos son los correspondientes adjuntos de los elementos de una matriz cuadrada
 se llama matriz adjunta de
se llama matriz adjunta de
 y se denota por
y se denota por
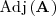 .
El elemento en la i-esima fila y j-esima columna de la matriz adjunta de
.
El elemento en la i-esima fila y j-esima columna de la matriz adjunta de
 es
es
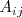 ,
el adjunto del elemento de
,
el adjunto del elemento de
 en su fila i-esima y columna j-esima
en su fila i-esima y columna j-esima
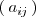 .
.
Ejemplo
Los menores complementarios de los elementos de la matriz
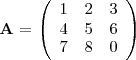
son
![\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-a36be844309df6d93b47dcee845bf84c.png)
![\begin{array}{ccc}
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}{ccc}
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 0
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-98ca9991fa3be632c20040173a4b60a3.png)
![\begin{array}{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-ae0a951832e1ad291ba09451890262cb.png)
Los adjuntos de los elementos de
 son:
son:

La matriz adjunta de
 es
es
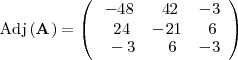
El determinante de
 lo podemos calcular desarrollando por la primera fila:
lo podemos calcular desarrollando por la primera fila:
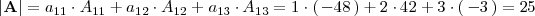
Por lo tanto, la matriz inversa de
 es
es
![\mathbf{A}^{-1} = \frac{1}{\left| \mathbf{A} \right|} \cdot
</p>
<pre>\left[
\makebox{Adj}
\left(
\, \mathbf{A} \,
\right)
\right]
^t =
\frac{1}{25} \cdot
\left(
\begin{array}{ccc}
</pre>
<p>-48 & ~24 & -3
\\
~42 & -21 & ~6
\\
~-3 & ~~6 & -3
\end{array}
\right)
\mathbf{A}^{-1} = \frac{1}{\left| \mathbf{A} \right|} \cdot
</p>
<pre>\left[
\makebox{Adj}
\left(
\, \mathbf{A} \,
\right)
\right]
^t =
\frac{1}{25} \cdot
\left(
\begin{array}{ccc}
</pre>
<p>-48 & ~24 & -3
\\
~42 & -21 & ~6
\\
~-3 & ~~6 & -3
\end{array}
\right)](/images/math/math-481ad4c2bef5fcc6f50021ede0f7ba57.png)
Ejercicios resueltos
Producto e invertibilidad de matrices


![\mathbf{A}^{-1} = \frac{1}{\left| \mathbf{A} \right|} \cdot
\left[
\makebox{Adj}
\left(
\, \mathbf{A} \,
\right)
\right]
^t
\mathbf{A}^{-1} = \frac{1}{\left| \mathbf{A} \right|} \cdot
\left[
\makebox{Adj}
\left(
\, \mathbf{A} \,
\right)
\right]
^t](/images/math/math-c011b0bea45a431636f4149f1d52defa.png)

