Ángulo entre dos rectas
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | ==Ángulo entre | + | ==Ángulo entre una recta y un plano== |
<br/> | <br/> | ||
| - | El ángulo | + | El ángulo |
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | que forma una recta | ||
<math> | <math> | ||
r | r | ||
</math> | </math> | ||
| - | + | cuyo vector director es | |
<math> | <math> | ||
| - | + | \mathbf{u} | |
</math> | </math> | ||
| - | + | y un plano | |
<math> | <math> | ||
| - | + | \pi | |
</math> | </math> | ||
| - | + | cuyo ángulo normal es | |
<math> | <math> | ||
| - | + | \mathbf{n} | |
</math> | </math> | ||
| - | + | es complementario al ángulo que forman | |
| - | + | ||
<math> | <math> | ||
r | r | ||
| Línea 27: | Línea 30: | ||
y | y | ||
<math> | <math> | ||
| - | + | \mathbf{n} | |
| - | </math> | + | </math>. |
| - | + | ||
<br/> | <br/> | ||
| - | + | Por lo tanto, se tiene que | |
| + | <center> | ||
<math> | <math> | ||
| - | \alpha | + | \cos \left( \, 90 - \alpha \, \right) = |
| + | \frac{\left| \, \mathbf{n}, \, \mathbf{u} \, \right|}{\left| \, \mathbf{n} \, \right| \cdot \left| \, \mathbf{u} \, \right|}} | ||
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | Podemos obtener un vector director de la recta | ||
<math> | <math> | ||
| - | + | r | |
| - | </math> | + | </math> |
| + | multiplicando vectorialmente un vector perpendicular al plano: | ||
| + | <center> | ||
<math> | <math> | ||
| - | + | 0 = x - 2y + 3z | |
| - | </math> | + | </math> |
| - | + | </center> | |
| - | < | + | por un vector perpendicular del plano |
| - | + | ||
<center> | <center> | ||
| - | + | <math> | |
| + | 0 = 2x - y + 4 | ||
| + | </math> | ||
</center> | </center> | ||
| - | < | + | Un vector perpendicular al plano |
| - | + | <center> | |
| - | + | ||
<math> | <math> | ||
| - | + | 0 = x - 2y + 3z | |
</math> | </math> | ||
| - | y | + | </center> |
| + | lo podemos obtener de los coeficientes de x, y, z en la ecuacion anterior: | ||
| + | <center> | ||
<math> | <math> | ||
| - | + | \mathbf{n} = \left( \, 1, \, -2, \, 3 \, \right) | |
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | De la misma forma obtenemos un vector perpendicular al otro plano | ||
| + | <center> | ||
<math> | <math> | ||
| - | \mathbf{ | + | \mathbf{n^\prime} = \left( \, 2, \, -1, \, 0 \, \right) |
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | El producto vectorial de ambos vectores, | ||
| + | <math> | ||
| + | \mathbf{n} | ||
| + | </math> | ||
| + | y | ||
<math> | <math> | ||
| - | \mathbf{ | + | \mathbf{n}^\prime |
</math> | </math> | ||
| - | + | es | |
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left| | |
| - | + | \begin{array}{ccc} | |
| + | \mathbf{i} & \mathbf{j} & \mathbf{k} | ||
| + | \\ | ||
| + | 1 & -2 & 3 | ||
| + | \\ | ||
| + | 2 & -1 & 0 | ||
| + | \end{array} | ||
| + | \right| = \left( \, 3, \, -6, \, 3 \, \right) | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | donde la segunda fila es | |
| - | + | ||
<math> | <math> | ||
| - | + | \mathbf{n} | |
</math> | </math> | ||
| - | y | + | y la tercera es |
<math> | <math> | ||
| - | + | \mathbf{n}^\prime | |
</math>. | </math>. | ||
| + | |||
| + | <br/> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 12:16 24 oct 2010
Ángulo entre una recta y un plano
El ángulo
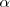 que forma una recta
que forma una recta
 cuyo vector director es
cuyo vector director es
 y un plano
y un plano
 cuyo ángulo normal es
cuyo ángulo normal es
 es complementario al ángulo que forman
es complementario al ángulo que forman
 y
y
 .
.
Por lo tanto, se tiene que
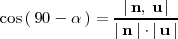
Podemos obtener un vector director de la recta
 multiplicando vectorialmente un vector perpendicular al plano:
multiplicando vectorialmente un vector perpendicular al plano:
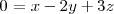
por un vector perpendicular del plano
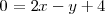
Un vector perpendicular al plano
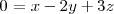
lo podemos obtener de los coeficientes de x, y, z en la ecuacion anterior:
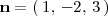
De la misma forma obtenemos un vector perpendicular al otro plano
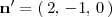
El producto vectorial de ambos vectores,
 y
y
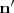 es
es
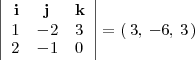
donde la segunda fila es
 y la tercera es
y la tercera es
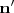 .
.



