Resolución de ecuaciones no lineales
De Wikillerato
(→Ecuaciones de segundo grado) |
m (Revertidas las ediciones realizadas por 83.55.39.106 (Talk); a la última edición de Fjmolina) |
||
| Línea 1: | Línea 1: | ||
| + | |||
<br/> | <br/> | ||
| Línea 8: | Línea 9: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | ax^2 + bx+ | + | ax^2 + bx + c = 0 |
</math> | </math> | ||
</center> | </center> | ||
Revisión actual
Tabla de contenidos |
Ecuaciones de segundo grado
Una ecuación de segundo grado es una ecuación del tipo:
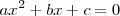
donde
 ,
,
 y
y
 son números reales.
son números reales.
Si
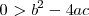 ,
entonces la ecuación de segundo grado no tiene solución.
,
entonces la ecuación de segundo grado no tiene solución.
Si
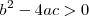 ,
entonces la ecuación tiene dos soluciones, que se pueden calcular con la
siguiente formula:
,
entonces la ecuación tiene dos soluciones, que se pueden calcular con la
siguiente formula:
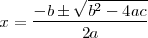
Esta formula tambien se puede utilizar cuando
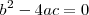 ,
pero, en este caso, en vez de tener dos soluciones, la ecuación de
segundo grado solo tiene una solución.
,
pero, en este caso, en vez de tener dos soluciones, la ecuación de
segundo grado solo tiene una solución.
Ecuaciones bicuadradas
Una ecuación bicuadrada es una ecuación del tipo:
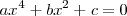
donde
 ,
,
 y
y
 son números reales.
son números reales.
Para resolverla efectuamos el cambio de incognita
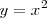 Con este cambio de incognita, nos queda que
Con este cambio de incognita, nos queda que
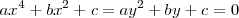
Resolvemos la ecuación de segundo grado
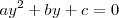
y para cada solución positiva
 de esta ecuación, habra dos soluciones de la ecuación bicuadratica
de partida:
de esta ecuación, habra dos soluciones de la ecuación bicuadratica
de partida:
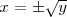 .
.
Ejemplo 1
Resolvamos la ecuación
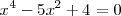
Lo primeros que hacemos es realizar el cambio de incognita
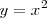 en la ecuación anterior, obteniendo de esta forma la ecuacion en
en la ecuación anterior, obteniendo de esta forma la ecuacion en
 :
:
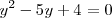
Cuyas soluciones se calculan de la siguiente manera:
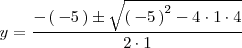
obteniendose las soluciones
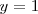 e
e
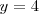 .
.
Por lo tanto las soluciones de la ecuación bicuadrada de este ejemplo son:
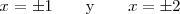
( cuatro soluciones )
Ecuaciones con radicales
Para resolver ecuaciones en las que la incognita  se encuentra bajo una raiz cuadrada se siguen los siguientes pasos:
se encuentra bajo una raiz cuadrada se siguen los siguientes pasos:
- 1. se aisla la raiz cuadrada con el
 dentro, y
dentro, y
- 2. se eleva al cuadrado ambos miembros de la ecuación.
Cada una de las soluciones de la ecuación obtenida de esta forma puede ser o no solución de la ecuación inicial que queremos resolver. Para comprobar si lo es sustituimos la posible solución en la ecuación de partida. Si obtenemos una identidad, entonces se trata de una solución. En caso contrario no se trata de una solución.
Ejemplo 2
Resolvamos la ecuación
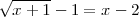
Lo primero que hacemos es dejar la raiz cudrada
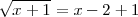
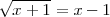
y a continuación elevamos al cuadrado ambos miembros de la ecuación
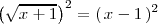
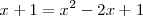
Agrupando todos los terminos en un solo miembro y dejando cero en el otro, obtenemos la siguiente ecuación de segundo grado:
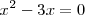
Esta ecuación de segundo grado tiene dos soluciones, 0 y 3. Para comprobar
si el 0 es solución de la ecuación partida, sustituimos
 por 0 en dicha ecuación y obtenemos
por 0 en dicha ecuación y obtenemos
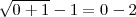
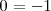
como esto no es cierto,
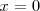 no es solución.
no es solución.
Hagamos ahora lo mismo con
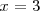 :
:
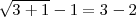
Como esta igualdad se cumple, 3 si que es solución de
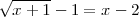
Ecuaciones con x en el denominador
Cuando en una ecuación tengamos fracciones, para resolver la ecuación se puede multiplicar esta por el minimo común multiplo de los denominadores de las fracciones. De esta manera desaparecerian las fracciones de la ecuación.
Las soluciones de la ecuación asi obtenida puede ser o no ser solución de la ecuación inicial con fracciones, por lo que habra que comprobar que las soluciones de la ecuación obtenida multiplicando cada miembro por el minimo común multiplo de los denominadores es solución tambien de la ecuación de partida.
Ejemplo 3
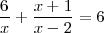
En este caso el minimo comúm multiplo de los denominadores es
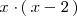 .
Multiplicando la ecuación por
.
Multiplicando la ecuación por
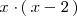 ( ambos miembros ), se obtiene la ecuación
( ambos miembros ), se obtiene la ecuación
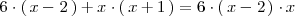
que es una ecuación cuadratica
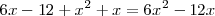
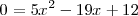
cuyas soluciones son
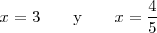
Sustituyendo estos valores en la ecuación inicial se compruba facilmente que ambos son soluciones de esta ecuación:
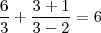
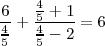
Ecuaciones exponenciales
Las ecuaciones exponenciales son aquellas en las que la incognita esta en el exponente.
Ejemplo 4
La ecuación
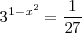
es una ecuación exponencial. Se puede resolver tomando logaritmos en base 3 en ambos miembros:
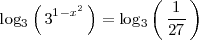
Como
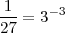 y como
y como
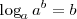
para cualquier número real
 ,
la ecuación anterior es equivalente a esta otra
,
la ecuación anterior es equivalente a esta otra
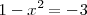
que es una ecuación de segundo grado.
Ejemplo 5
Consideremos ahora la ecuación exponencial
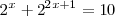
Para resolver esta ecuacion realizamos el cambio de incognita
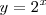 .
.
Con este cambio de incognita, la ecuacion anterior es equivalente a esta otra
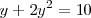
que es una ecuación de segundo grado.
Notese que, por las propiedades de las potencias
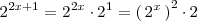
Las soluciones de la ecuación de segundo grado anterior son
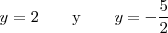
Como no existe ningún número real
 tal que
tal que
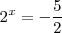 nos quedamos solo con la solución
nos quedamos solo con la solución
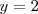 :
:
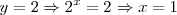
Por lo tanto
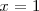 es la unica solución de la ecuación de partida:
es la unica solución de la ecuación de partida:
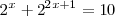
Ecuaciones logaritmicas
Es facil imaginarse lo que puede ser una ecuación logaritmica, ¿no? Dejemos volar la imaginación.
Ejemplo 6
La ecuación
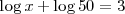
es una ecuación logaritmica.
Por las propiedades de los logaritmos (
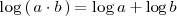 ):
):
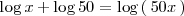
Por otra parte, por la definición de logaritmo ( decimal )
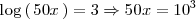
con lo cual, la solución es
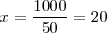
Ejemplo 7
Para resolver la ecuación logaritmica
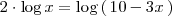
utilizamos, de nuevo, las propidades de los logaritmos, en concreto la propiedad
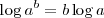
por la cual
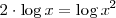
Por lo tanto
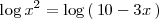
Por la siguiente propiedad de los logaritmos
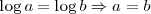
se tiene que
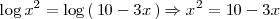
siendo esta ultima ecuación una ecuación de segundo grado cuyas soluciones son 2 y -5, que son tambien las soluciones de la ecuación logaritmica que queriamos resolver.
Tweet


