Integrales inmediatas
De Wikillerato
(Diferencias entre revisiones)
| Línea 2: | Línea 2: | ||
<br/> | <br/> | ||
| - | |||
<center> | <center> | ||
| - | {| style="margin:1em 1em 1em 0;background: #f9f9f9;border:2px # | + | {| style="margin:1em 1em 1em 0;background: #f9f9f9;border:2px #00aaaaa solid;border-collapse: collapse;" border="1" cellpadding="4" cellspacing="2" |
| Línea 11: | Línea 10: | ||
! función <math>f \,\!</math>: derivada de <math>F \,\!</math> | ! función <math>f \,\!</math>: derivada de <math>F \,\!</math> | ||
|- | |- | ||
| - | || <math>f\left(x\right) = \frac {x^{n+1}}{n+1} + k \,\!</math> | + | || <math>f\left(x\right) = \frac {x^{n+1}}{n+1} + k \,\!</math> |
| - | || <math>\begin{matrix}f'\left(x\right) = x^n & & \mathrm{ , para} & n \neq -1 \end{matrix} \,\!</math> | + | || <math>\begin{matrix}f'\left(x\right) = x^n & & \mathrm{ , para} & n |
| + | \neq -1 \end{matrix} \,\!</math> | ||
|- | |- | ||
| - | || <math>f\left(x\right) = e^x + k \,\!</math> | + | || <math>f\left(x\right) = e^x + k \,\!</math> |
| - | || <math>f'\left(x\right) = e^x \,\!</math> | + | || <math>f'\left(x\right) = e^x \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = \ln\left(x\right) + k \,\!</math> | + | || <math>f\left(x\right) = \ln\left(x\right) + k \,\!</math> |
| - | || <math>f'\left(x\right) = \frac{1}{x} \,\!</math> | + | || <math>f'\left(x\right) = \frac{1}{x} \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = \frac {x^{1-n}}{1-n} + k \,\!</math> | + | || <math>f\left(x\right) = \frac {x^{1-n}}{1-n} + k \,\!</math> |
| - | || <math>\begin{matrix}f'\left(x\right) = \frac {1}{x^n} & & \mathrm{ , para} & n \neq 1 \end{matrix} \,\!</math> | + | || <math>\begin{matrix}f'\left(x\right) = \frac {1}{x^n} & & \mathrm{ , para} & n \neq 1 \end{matrix} \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = -\cos\left(x\right) + k \,\!</math> | + | || <math>f\left(x\right) = -\cos\left(x\right) + k \,\!</math> |
| - | || <math>f'\left(x\right) = \sin\left(x\right) \,\!</math> | + | || <math>f'\left(x\right) = \sin\left(x\right) \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = \sin\left(x\right) + k \,\!</math> | + | || <math>f\left(x\right) = \sin\left(x\right) + k \,\!</math> |
| - | || <math>f'\left(x\right) = \cos\left(x\right) \,\!</math> | + | || <math>f'\left(x\right) = \cos\left(x\right) \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = \tan\left(x\right) + k \,\!</math> | + | || <math>f\left(x\right) = \tan\left(x\right) + k \,\!</math> |
| - | || <math>f'\left(x\right) = \frac {1}{\cos^2\left (x\right)} \,\!</math> | + | || <math>f'\left(x\right) = \frac {1}{\cos^2\left (x\right)} \,\!</math> |
|- | |- | ||
| - | || <math>\begin{matrix}f\left(x\right) = \frac {a^x}{\ln(a)} + k & & \mathrm{, si} & a > 0 \end{matrix} \,\!</math> | + | || <math>\begin{matrix}f\left(x\right) = \frac {a^x}{\ln(a)} + k & & |
| - | || <math>f'\left(x\right) = a^x \,\!</math> | + | \mathrm{, si} & a > 0 \end{matrix} \,\!</math> |
| + | || <math>f'\left(x\right) = a^x \,\!</math> | ||
|- | |- | ||
| - | ||<math> f\left(x\right) = \frac {2}{3} \sqrt{x}^3 + k \,\!</math> | + | || <math> f\left(x\right) = \frac {2}{3} \sqrt{x}^3 + k \,\!</math> |
| - | || <math>f'\left(x\right) = \sqrt {x} \,\!</math> | + | || <math>f'\left(x\right) = \sqrt {x} \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = ax + k \,\!</math> | + | || <math>f\left(x\right) = ax + k \,\!</math> |
| - | || <math>f'\left(x\right) = a \,\!</math> | + | || <math>f'\left(x\right) = a \,\!</math> |
|- | |- | ||
| - | || <math>f\left(x\right) = \arctan(x) + k \,\!</math> | + | || <math>f\left(x\right) = \arctan(x) + k \,\!</math> |
| - | || <math>f'\left(x\right) = \frac{1}{1+x^2} \,\!</math> | + | || <math>f'\left(x\right) = \frac{1}{1+x^2} \,\!</math> |
|} | |} | ||
</center> | </center> | ||
[[Category: Matemáticas]] | [[Category: Matemáticas]] | ||
Revisión de 21:54 15 nov 2010
Aquí están las principales funciones primitivas:
Función 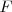 : primitiva de : primitiva de 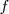
| función 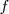 : derivada de : derivada de 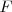
|
|---|---|
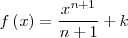
| 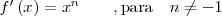
|
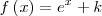
| 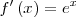
|
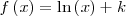
| 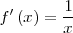
|
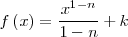
| 
|
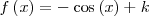
| 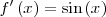
|
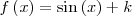
| 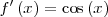
|
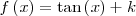
| 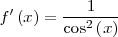
|
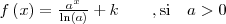
| 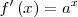
|
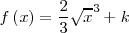
| 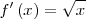
|
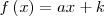
| 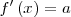
|
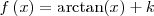
| 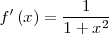
|



