Navegación
Aceleración
De Wikillerato
| Línea 17: | Línea 17: | ||
Teniendo en cuenta que: | Teniendo en cuenta que: | ||
| - | <math> vec v = v_x\vec i + v_y\vec j + v_z\vec k</math> | + | <math> \vec v = v_x\vec i + v_y\vec j + v_z\vec k</math> |
si derivamos, se obtiene: | si derivamos, se obtiene: | ||
| - | <math>\vec a = frac{d v_x\vec i + v_y\vec j + v_z\vec k}{dt}</math> | + | <math>\vec a = \frac{d v_x\vec i + v_y\vec j + v_z\vec k}{dt}</math> |
| - | <math>\vec a = frac{d v_x}{dt} \vec i+ frac{d v_y}{dt} \vec j + frac{d vec v_z}{dt} \vec k</math> | + | <math>\vec a = \frac{d v_x}{dt} \vec i+ frac{d v_y}{dt} \vec j + frac{d vec v_z}{dt} \vec k</math> |
con lo cual: | con lo cual: | ||
Revisión de 12:16 4 dic 2006
Llamamos aceleración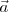 
a la variación temporal del vector velocidad, es decir:
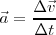
En el caso en el que la variación de la velocidad no sea constante, al cociente
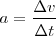
se le denomina aceleración media.
En este caso, si consideramos intervalos de tiempo instantáneos, podremos hablar de aceleración instantánea y se podrá definir mediante la ecuación,
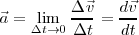
La aceleración media es un escalar, pues no podemos atribuirle una dirección, dado que la variación temporal de v no es constante. Sin embargo, la aceleración instantánea es una magnitud vectorial, pues nos proporciona las variaciones del vector velocidad en un instante preciso. En el SI las unidades en que se expresa la aceleración es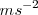 
, pues se obtiene de dividir una diferencia de velocidades entre un tiempo preciso, 
.
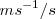Teniendo en cuenta que:
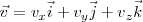
si derivamos, se obtiene:
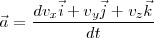
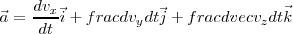
con lo cual:
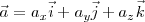
Que es la expresión de la aceleración en un instante dado en función de sus componentes en un sistema ortogonal tridimensional.
Tweet
