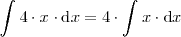Propiedades de las integrales indefinidas
De Wikillerato
(Diferencias entre revisiones)
| Línea 2: | Línea 2: | ||
==Propiedad 1== | ==Propiedad 1== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{f} \left( \, x \, \right) \cdot \mathrm{d}x = \mathrm{f} \left( \, | ||
| + | x \, \right) + C | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Propiedad 2== | ||
<br/> | <br/> | ||
| Línea 39: | Línea 52: | ||
<br/> | <br/> | ||
| - | ==Propiedad | + | ==Propiedad 3== |
<br/> | <br/> | ||
Revisión de 09:57 30 dic 2010
Tabla de contenidos |
Propiedad 1
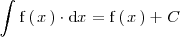
Propiedad 2
La integral de la suma de dos funciones es igual a la suma de las integrales de dichas funciones:
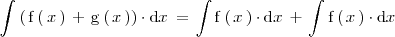
Ejemplo
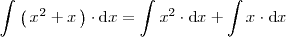
Propiedad 3
La integral indefinida del producto de un número realpor una función
es igual al producto de
por la integral indefinida de
:
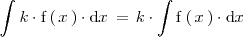
Ejemplo