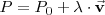|
|
| Línea 45: |
Línea 45: |
| | \lambda \in R | | \lambda \in R |
| | </math> | | </math> |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Dado un triángulo rectángulo, podemos estudiar las razones o proporciones entre sus
| |
| - | lados.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | [[Image:triangulo.gif]]
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Estas razones las definimos asociadas a cada uno de sus angulos de la siguiente
| |
| - | forma:
| |
| - |
| |
| - | El seno de un ángulo, es la razon entre su cateto opuesto y la hipotenusa. Su inversa es
| |
| - | la cosecante:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \mathrm{sen} \, \alpha = \frac{\makebox{cateto opuesto}}{\makebox{hipotenusa}}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \mathrm{cosec} \, \alpha = \frac{\makebox{hipotenusa}}{\makebox{cateto opuesto}}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | El coseno de un ángulo, es la razon entre su cateto contiguo y la hipotenusa. Su inversa
| |
| - | es la secante:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \cos \alpha = \frac{\makebox{cateto contiguo}}{\makebox{hipotenusa}}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \sec \alpha = \frac{\makebox{hipotenusa}}{\makebox{cateto contiguo}}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | La tangente de un ángulo, es la razon entre su cateto opuesto y su cateto contiguo. Su
| |
| - | inversa es la contangente:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \mathrm{tg} \, \alpha = \frac{\makebox{cateto opuesto}}{\makebox{cateto contiguo}}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \mathrm{cotg} \, \alpha = \frac{\makebox{cateto contiguo}}{\makebox{cateto opuesto}}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Para el estudio de las razones trigonometricas se suele considerar el angulo
| |
| - | <math>
| |
| - | \alpha
| |
| - | </math>
| |
| - | que forma el eje
| |
| - | <math>
| |
| - | X
| |
| - | </math>
| |
| - | con el radio de una circunferencia de radio
| |
| - | <math>
| |
| - | 1
| |
| - | </math>
| |
| - | y centrada en el origen de coordenadas. A esta circunferencia se le llama
| |
| - | circunferencia goniometrica.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | [[Image:circulo.gif]]
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | En este caso
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \mathrm{sen} \, \alpha = y \qquad \mathrm{cosec} \, \alpha = \frac{1}{y} \qquad
| |
| - |
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \cos \alpha = x \qquad \sec \alpha = \frac{1}{x}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \mathrm{tg} \, \alpha = \frac{y}{x} \qquad \mathrm{cotg} \, \alpha = \frac{x}{y}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | El angulo
| |
| - | <math>
| |
| - | \alpha
| |
| - | </math>
| |
| - | aumenta sii movemos el punto
| |
| - | <math>
| |
| - | P
| |
| - | </math>
| |
| - | en la circunferencia de manera que el radio
| |
| - | <math>
| |
| - | \overline{OP}
| |
| - | </math>
| |
| - | gire en sentido contrario al de las las agujas del reloj.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Si
| |
| - | <math>
| |
| - | P
| |
| - | </math>
| |
| - | esta a la derecha del eje
| |
| - | <math>
| |
| - | Y,
| |
| - | </math>
| |
| - | entonces
| |
| - | <math>
| |
| - | x > 0.
| |
| - | </math>
| |
| - | En caso contrario, se tiene que
| |
| - | <math>
| |
| - | x < 0.
| |
| - | </math>
| |
| - | Si
| |
| - | <math>
| |
| - | P
| |
| - | </math>
| |
| - | esta por encima del eje
| |
| - | <math>
| |
| - | X,
| |
| - | </math>
| |
| - | entonces
| |
| - | <math>
| |
| - | y > 0.
| |
| - | </math>
| |
| - | En caso contrario, se tiene que
| |
| - | <math>
| |
| - | y < 0.
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Los ejes de coordenadas dividen la circunferencia goniometrica en cuatro cuadrantes. El
| |
| - | signo de las razones de un angulo
| |
| - | <math>
| |
| - | \alpha
| |
| - | </math>
| |
| - | depende de en que cuadrante este situado
| |
| - | <math>
| |
| - | P
| |
| - | </math>
| |
| - | . Todas las posibilidades estan recogidas en la tabla siguiente:
| |
| | | | |
| | <br/> | | <br/> |
| Línea 270: |
Línea 77: |
| | | | |
| | <math> | | <math> |
| - | \stackrel{\longrightarrow}{OP} | + | \stackrel{\longrightarrow}{OP}, |
| | </math> | | </math> |
| - | , se tiene que
| + | se tiene que |
| | <math> | | <math> |
| | P = P_0 + \lambda \cdot \vec{\mathbf{v}} | | P = P_0 + \lambda \cdot \vec{\mathbf{v}} |
| | </math> | | </math> |
Al igual que ocurre en el plano, una recta en el espacio queda determinada conociendo un
punto
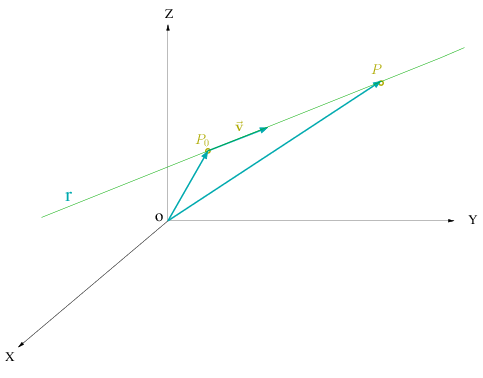
 y un vector no nulo
y un vector no nulo
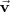 que se llama vector director o direccional de la recta.
que se llama vector director o direccional de la recta.
Estudiamos a continuacion las diferentes formas que puede adoptar la ecuacion de una
recta.
 y un vector no nulo
y un vector no nulo
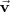 que se llama vector director o direccional de la recta.
que se llama vector director o direccional de la recta.
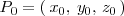 y tiene por vector director
y tiene por vector director
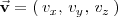 es el conjunto de puntos
es el conjunto de puntos
 del espacio que verifican la relacion vectorial
del espacio que verifican la relacion vectorial
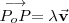 con
con
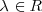
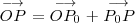
 con el vector que va desde el origen de coordenadas hasta el punto
con el vector que va desde el origen de coordenadas hasta el punto
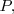 [Unparseable or potentially dangerous latex formula. Error 3 ]
se tiene que
[Unparseable or potentially dangerous latex formula. Error 3 ]
se tiene que