Navegación
Curvas técnicas
De Wikillerato
m (Revertidas las ediciones realizadas por 83.45.74.74 (Talk); a la última edición de 85.56.48.248) |
(→Curvas cíclicas) |
||
| Línea 21: | Línea 21: | ||
===Curvas cíclicas=== | ===Curvas cíclicas=== | ||
| - | + | son curvas las cuales solo usan los ciclistas y los citricos como el pomelo o naranja e incluso a veces el limon. | |
| - | + | su uso cotidiano es simplemente para saber cuanto t mide el agujero del culo, o el de la nariz | |
| - | [[ | + | [[http://2.bp.blogspot.com/_TswPaQyBm_A/TU9GRl7G79I/AAAAAAAAAsc/t9qt8cvm_XU/s1600/FUCKYOU.jpg]] |
===Otras curvas=== | ===Otras curvas=== | ||
Revisión de 15:51 7 mar 2011
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Concepto de curva técnica
Son curvas de aplicación en la ingeniería y en la arquitectura.
Óvalos y ovoides
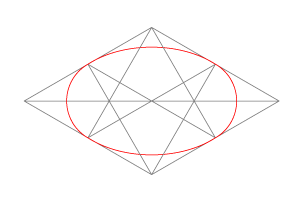
Son curvas técnicas formadas por circunferencias tangentes entre sí: con forma de huevo (ovoides) o con forma parecida a la de las elipses (óvalos).
En la figura vemos un óvalo inscrito en un rombo.
Espirales, volutas y evolventes
Son curvas técnicas, engendradas por un punto que se aleja o se acerca a su origen según se mueva en uno u otro sentido. Algunas están formadas por arcos de circunferencia (como las espirales de centros alineados, las de centros en los vértices de polígonos, regulares o no, las volutas y las espirales áurea y logarítmica). Otras espirales son representaciones de trayectorias, como la espiral de Arquímedes y la evolvente de la circunferencia.
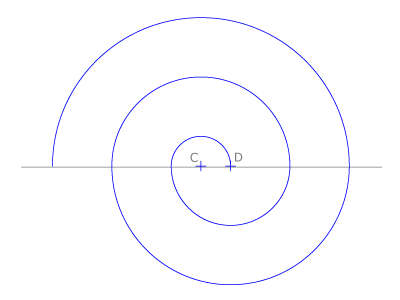
En la figura vemos la espiral más sencilla, la de Honnecourt, con dos centros.
Curvas cíclicas
son curvas las cuales solo usan los ciclistas y los citricos como el pomelo o naranja e incluso a veces el limon. su uso cotidiano es simplemente para saber cuanto t mide el agujero del culo, o el de la nariz
[[1]]
Otras curvas
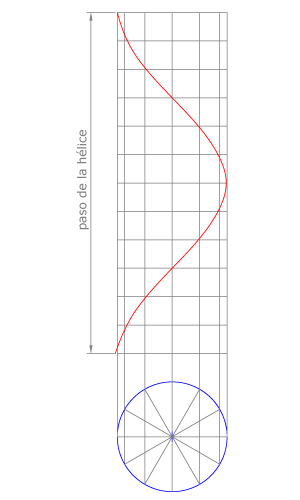
La hélice cilíndrica, que no es una curva plana, también se estudia por ser de gran aplicación en arquitectura (escaleras de caracol) y en ingeniería (formas helicoidales).
![[1]](http://2.bp.blogspot.com/_TswPaQyBm_A/TU9GRl7G79I/AAAAAAAAAsc/t9qt8cvm_XU/s1600/FUCKYOU.jpg){kind=link}