Eje radical de dos circunferencias
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
Ver antes [[Concepto_de_potencia]] | Ver antes [[Concepto_de_potencia]] | ||
| + | |||
| + | |||
| + | == Eje radical de dos circunferencias == | ||
| + | |||
Al igual que existe un punto P que tiene una cierta potencia respecto de una circunferencia, existe una recta que tiene igual potencia respecto de dos circunferencias, de centros O1 y O2. | Al igual que existe un punto P que tiene una cierta potencia respecto de una circunferencia, existe una recta que tiene igual potencia respecto de dos circunferencias, de centros O1 y O2. | ||
| Línea 5: | Línea 9: | ||
Para las diversas posiciones relativas de las circunferencias, existen diferentes maneras de obtener el eje radical: | Para las diversas posiciones relativas de las circunferencias, existen diferentes maneras de obtener el eje radical: | ||
| - | '''Eje | + | '''Eje radical de dos circunferencias secantes''' |
Es la recta que resulta de unir los puntos 1 y 2, resultantes de la intersección de ambas circunferencias: | Es la recta que resulta de unir los puntos 1 y 2, resultantes de la intersección de ambas circunferencias: | ||
Revisión de 21:19 12 dic 2006
Ver antes Concepto_de_potencia
Eje radical de dos circunferencias
Al igual que existe un punto P que tiene una cierta potencia respecto de una circunferencia, existe una recta que tiene igual potencia respecto de dos circunferencias, de centros O1 y O2.
Para las diversas posiciones relativas de las circunferencias, existen diferentes maneras de obtener el eje radical:
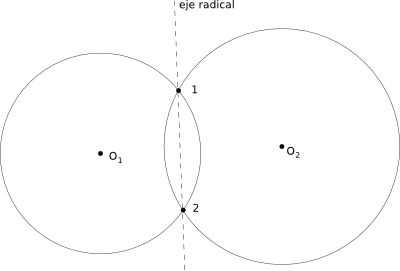
Eje radical de dos circunferencias secantes
Es la recta que resulta de unir los puntos 1 y 2, resultantes de la intersección de ambas circunferencias:
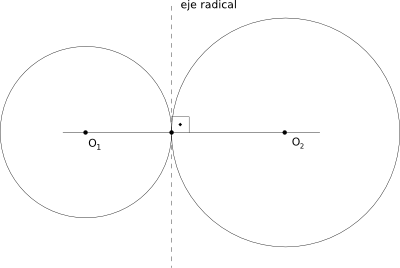
Circunferencias tangentes
Si las circunferencias son tangentes, 1 y 2 serán el mismo punto, por lo que el eje radical pasará por el punto de tangencia de las dos circunferencias, y será perpendicular a la recta que uno los centros de estas:
Tweet