Problemas de distancias
De Wikillerato
(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 118.139.160.154 (Talk); a la última edición de 193.48.0.3) |
|||
| Línea 24: | Línea 24: | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
==Distancia de una recta a un plano== | ==Distancia de una recta a un plano== | ||
| Línea 141: | Línea 137: | ||
<br/> | <br/> | ||
| - | |||
| - | |||
Revisión de 08:00 4 jul 2011
Distancia entre dos puntos
La distancia entre dos puntos
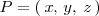 y
y
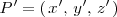 es
es
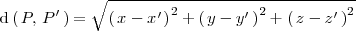
Distancia de una recta a un plano
Sea
 una recta paralela a un plano
una recta paralela a un plano
 .
.
Para calcular la distancia de
 a
a
 lo unico que tenemos que hacer es encontrar un punto
lo unico que tenemos que hacer es encontrar un punto
 en la recta
en la recta
 y calcular la distancia de este punto al plano
y calcular la distancia de este punto al plano
 .
.
Distancia entre dos rectas
Para calcular la distancia entre dos rectas,
 y
y
 ,
que se cruzan se procede de la siguiente manera:
,
que se cruzan se procede de la siguiente manera:
En primer lugar, se encuentran vectores directores de ambas rectas,
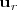 y
y
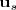 , y un par de puntos,
, y un par de puntos,
 y
y
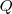 ,
en
,
en
 y en
y en
 ,
respectivamente.
,
respectivamente.
A continuación, se calcula la longitud de la proyección del vector
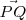 en la dirección normal a un plano paralelo a
en la dirección normal a un plano paralelo a
 y a
y a
 . Esta dirección es la del vector
. Esta dirección es la del vector
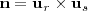
La distancia que buscamos la podemos cacular con la formula