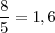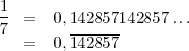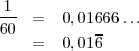Números racionales
De Wikillerato
(→Notación) |
|||
| Línea 33: | Línea 33: | ||
* <math>\frac{a}{b}\left(\frac{c}{d}\right)</math> denota a <math>\frac{a}{b}\times\frac{c}{d}</math> | * <math>\frac{a}{b}\left(\frac{c}{d}\right)</math> denota a <math>\frac{a}{b}\times\frac{c}{d}</math> | ||
| - | * Todo número <math>\frac{p}{1}</math> se denota simplemente por <math> p \, </math>. Dichos números conforman el conjunto de los números naturales <math> \mathbb{N} </math>, y | + | * Todo número <math>\frac{p}{1}</math> se denota simplemente por <math> p \, </math>. Dichos números conforman el conjunto de los números naturales <math> \mathbb{N} </math>, y están incluidos en el conjunto de los números racionanes <math> \mathbb{Q} </math> |
== Propiedades de los números racionales == | == Propiedades de los números racionales == | ||
Revisión de 08:11 4 jul 2011
Tabla de contenidos |
Definición de número racional
Se llama número racional a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero (una fracción común).
En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de todas ellas, se toma como representante de dicho número racional a la [fracción irreducible].
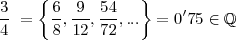
Definición formal
Definimos un número racional como un decimal finito o infinito periódico (por ejemplo, el número decimal finito 0,75 es la representación decimal del número racional 3/4. El número decimal infinito periódico 0,333... es la representación decimal del número racional 1/3). El número racional permite resolver ecuaciones del tipo ax = b, cuando a y b son números enteros (con «a» distinto de cero).
El conjunto de los números racionales se denota por 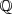 , que significa «cociente». Este conjunto de números incluye a los número enteros
, que significa «cociente». Este conjunto de números incluye a los número enteros 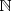 , y es un subconjunto de los números reales
, y es un subconjunto de los números reales 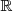 .
.
Construcción de los números racionales
- Consideremos las parejas de números enteros
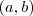 donde
donde 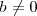 .
.
-
 denota a
denota a 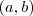 . A
. A  se le llama numerador y a
se le llama numerador y a 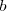 se le llama denominador
se le llama denominador
- Al conjunto de estos números se le denota por
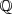 . Es decir
. Es decir 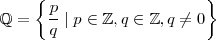
Suma y multiplicación en Q
- Se define la suma
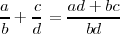
- Se define la multiplicación
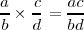
Notación
- Los números de tipo
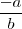 son denotados por
son denotados por 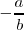
- Las sumas de tipo
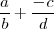 son denotadas por
son denotadas por 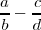
-
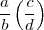 denota a
denota a 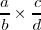
- Todo número
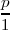 se denota simplemente por
se denota simplemente por 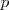 . Dichos números conforman el conjunto de los números naturales
. Dichos números conforman el conjunto de los números naturales 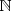 , y están incluidos en el conjunto de los números racionanes
, y están incluidos en el conjunto de los números racionanes 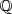
Propiedades de los números racionales
El conjunto de los números racionales con la suma y multiplicación definida de esta manera forman un Cuerpo.
Propiedades de la suma y multiplicación
- La suma en Q es conmutativa, esto es:
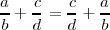
- La suma en Q es asociativa, esto es:
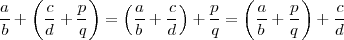
- La multiplicación en Q es asociativa, esto es:
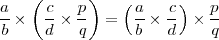
- La multiplicación se distribuye en la suma, esto es
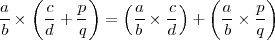
El conjunto de los números decimales en Q
- Un número decimal es un número racional de la forma
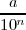
-
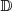 denota al conjunto de los números de este tipo. Es decir
denota al conjunto de los números de este tipo. Es decir 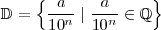
- Expresión Racional de un número decimal: el número
 en base
en base 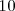 con un punto a
con un punto a  lugares del extremo derecho, por ejemplo
lugares del extremo derecho, por ejemplo 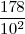 se denota como
se denota como 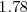
Representación decimal de los números racionales
Los números racionales se caracterizan por tener un desarrollo decimal cuya expresión sólo puede ser de tres tipos:
- Exacta: la parte decimal tiene un número finito de cifras. Ejemplo:
- Periódica pura: toda la parte decimal se repite indefinidamente. Ejemplo:
- Periódica mixta: no toda la parte decimal se repite. Ejemplo:
- Decimales exactos o finitos: Se escribe en el numerador la expresión decimal sin la coma (como un número entero), y en el denominador un uno seguido de tantos ceros como cifras decimales. Ejemplo:
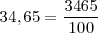
- Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma, y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo. Ejemplo:
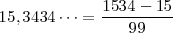
- Decimales periódicos mixtos: Tendrá como numerador la diferencia entre
 y
y 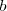 , donde
, donde  es el número escrito sin la coma, y
es el número escrito sin la coma, y 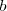 es el número sin la parte decimal periódica, escritos ambos como números enteros. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya. Ejemplo: Sea el número
es el número sin la parte decimal periódica, escritos ambos como números enteros. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya. Ejemplo: Sea el número 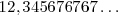 entonces
entonces 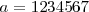 y
y 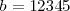 , por lo que el número buscado será
, por lo que el número buscado será 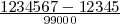 .
.