Regla de Cramer

De Wikillerato

(Diferencias entre revisiones)

Revisión de 23:54 18 ago 2011

Este artículo o sección necesita una revisión de gramática, ortografía o estilo.
Cuando se haya corregido, borra esta plantilla, por favor.

Gabriel Cramer nació en Ginebra (Suiza) en 1704 y murió en 1752. A él le debemos la regla que lleva su nombre. ¡Gracias Gabriel por tu contribución a las Matemáticas!

Esta regla, que lleva el nombre de este matemático suizo, es un método de resolución de sistemas de ecuaciones lineales que se puede utilizar cuando la matriz, $A$ , de coeficientes del sistema, es cuadrada y tiene determinante no nulo. El hecho de que la matriz $A$ sea cuadrada significa que el número de incógnitas y el número de ecuaciones del sistema coinciden.

Cuando el sistema de ecuaciones:

$\left. <pre> \begin{array}{c} a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1 \\ a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2 \\ \dotfill \\ a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m \end{array} </pre> \right\}$

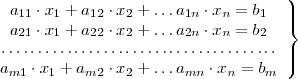
satisface las condiciones arriba mencionadas, su solución viene dada por:

$x_1 \, = \, \frac { <pre> \left| \begin{array}[c]{cccc} b_1 & a_{12} & \ldots & a_{1n} \\ b_2 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_m & a_{m2} & \ldots & a_{mn} \end{array} \right| </pre> } {|A|} , \qquad \qquad x_2 \, = \, \frac { <pre> \left| \begin{array}[c]{cccc} a_{11} & b_1 & \ldots & a_{1n} \\ a_{21} & b_2 & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & b_m & \ldots & a_{mn} \end{array} \right| </pre> } {|A|}, \qquad \qquad \ldots \ldots$

$\ldots \ldots, \qquad \qquad x_n \, = \, \frac { <pre> \left| \begin{array}[c]{cccc} a_{11} & a_{12} & \ldots & b_1 \\ a_{21} & a_{22} & \ldots & b_2 \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \ldots & b_m \end{array} \right| </pre> } {|A|} \qquad \qquad$

En general:

$x_i \, = \, \frac{|A_i|}{|A|}$

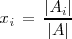
donde 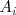$A_i$ es la matriz que se obtiene sustituyendo la i-ésima columna de $A$ por la matriz de los terminos independientes, $B$ .

Ejemplo

Consideremos el sistema de ecuaciones:

$\left\{ <pre> \begin{array}[c]{rcl} x \, + \, y \, = \, 2 \\ x \, - \, y \, = \, 0 \end{array} </pre> \right.$

En este sistema de ecuaciones lineales, la matriz $A$ de los coeficientes es una matriz cuadrada y $|A| \, = \, \left| <pre> \begin{array}[c]{cc} 1 & ~~1 \\ 1 & -1 \end{array} </pre> \right| <pre>\, = \, -2 \neq 0 </pre> $ . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:

$x \, = \, \frac { <pre> \left| \begin{array}[c]{cc} 2 & ~~1 \\ 0 & -1 \end{array} \right| </pre> } {|A|} \, = \, \frac{-2}{-2} \, = \, 1 \qquad \qquad y \, = \, \frac { <pre> \left| \begin{array}[c]{cc} 1 & 2 \\ 1 & 0 \end{array} \right| </pre> } {|A|}\, = \, \frac{-2}{-2} \, = \, 1$