El teorema de Euclides
De Wikillerato
(Página reemplazada por "polla") |
(Deshecha la edición por vandalismo) |
||
| Línea 1: | Línea 1: | ||
| - | + | Ya vimos el '''teorema de Euclides''', considerando su enunciados como teoremas de la '''altura''' y del '''cateto''', en el capítulo de triángulos y realizamos sus demostraciones gráficas. | |
| + | |||
| + | Ahora vamos a ver su relación con la '''tercera proporcional'''. Si consideramos que: | ||
| + | |||
| + | <math>\frac{a}{x}=\frac{x}{b}</math> | ||
| + | |||
| + | vemos que el término intermedio, '''x''', es media proporcional entre '''a''' y '''b''', pues: | ||
| + | |||
| + | <math>x^2 = ab</math> | ||
| + | |||
| + | Las construcciones de la media proporcional de dos segmentos, basadas directamente en '''Euclides''', tienen muchas aplicaciones en la resolución de problemas gráficos. | ||
| + | |||
| + | ==Aplicando el teorema de la altura== | ||
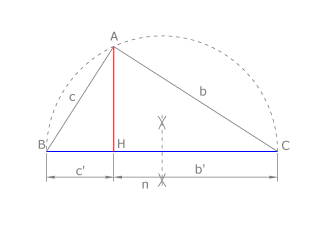
| + | Dibujamos el segmento '''BC= a+b''', como vemos en la figura. Trazamos la semicircunferencia de diámetro '''BC'''. Por el extremo común de los segmentos, '''H''', dibujamos la perpendicular a '''BC''' que corta al arco en '''A'''. | ||
| + | '''AH''' es la '''altura''' de '''ABC''' y es media proporcional de los segmentos en que divide a la hipotenusa: '''a y b''', como ya vimos en el capítulo 2. | ||
| + | |||
| + | <math>AH = \sqrt{ab}</math> | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 14.gif]] | ||
| + | |||
| + | ==Aplicando el teorema del cateto== | ||
| + | |||
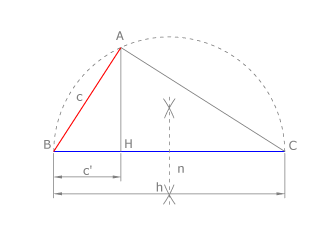
| + | Dibujamos el segmento '''BC=b''' y '''BH=a''', superpuestos, como vemos en la figura. Trazamos la semicircunferencia de diámetro '''BC'''. La perpendicular a '''BC''' desde '''H''' corta al arco en '''A'''. | ||
| + | |||
| + | El '''cateto AB''' es media proporcional su proyección sobre la hipotenusa, '''a''' , y de la hipotenusa, '''b''', como ya vimos en el capítulo 2. | ||
| + | |||
| + | <math>AB = \sqrt{ab}</math> | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 13.gif]] | ||
| + | |||
| + | ==Aplicaciones al cálculo gráfico== | ||
| + | |||
| + | Con el teorema de Euclides se puede hallar la raíz cuadrada de un producto de dos segmentos. | ||
| + | |||
| + | <h3>Enlaces externos</h3> | ||
| + | |||
| + | :[http://trazoide.com/proporcionalidad.html TRAZOIDE. Teoría y ejercicios resueltos de PROPORCIONALIDAD en Dibujo Técnico] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Ya vimos el teorema de Euclides, considerando su enunciados como teoremas de la altura y del cateto, en el capítulo de triángulos y realizamos sus demostraciones gráficas.
Ahora vamos a ver su relación con la tercera proporcional. Si consideramos que:
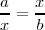
vemos que el término intermedio, x, es media proporcional entre a y b, pues:
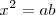
Las construcciones de la media proporcional de dos segmentos, basadas directamente en Euclides, tienen muchas aplicaciones en la resolución de problemas gráficos.
Tabla de contenidos |
Aplicando el teorema de la altura
Dibujamos el segmento BC= a+b, como vemos en la figura. Trazamos la semicircunferencia de diámetro BC. Por el extremo común de los segmentos, H, dibujamos la perpendicular a BC que corta al arco en A. AH es la altura de ABC y es media proporcional de los segmentos en que divide a la hipotenusa: a y b, como ya vimos en el capítulo 2.
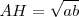
Aplicando el teorema del cateto
Dibujamos el segmento BC=b y BH=a, superpuestos, como vemos en la figura. Trazamos la semicircunferencia de diámetro BC. La perpendicular a BC desde H corta al arco en A.
El cateto AB es media proporcional su proyección sobre la hipotenusa, a , y de la hipotenusa, b, como ya vimos en el capítulo 2.
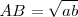
Aplicaciones al cálculo gráfico
Con el teorema de Euclides se puede hallar la raíz cuadrada de un producto de dos segmentos.