Buscar en WikilleratO
Temario:
Seleccionar asignatura
Matemáticas
Física
Filosofía
Lengua y Literatura
Dibujo Técnico
Historia
Historia del Arte
Química
Biología
Distribuciones discretas
De Wikillerato
(Diferencias entre revisiones)
Línea 1:
Línea 1: __TOC__
__TOC__
- ==Función de probabilidad==
+ ==Definicion ==
<br/>
<br/>
- Denotaremos como
+ Se llama '''''variable aleatoria''''' a toda aplicación
- <math>
+
- \mathrm{P}
+
- \left(
+
- \, X \, = \, x_i \,
+
- \right)
+
- </math>
+
- a la probabilidad de que la variable aleatoria tome el valor
+
- <math>
+
- x_i
+
- </math>
+
- .
+
-
+
- <br/>
+
-
+
- Se llama '''''función de probabilidad de una variable aleatoria discreta
+
<math>
<math>
X
X
</math>
</math>
- ''''' a la aplicacion que a cada valor de
+ del espacio muestral
<math>
<math>
- x_i
+ E
</math>
</math>
- de la variable le hace corresponder la probabilidad de que la variable tome dicho
+ en un subconjunto de los numeros reales :
- valor:
+
<br/>
<br/>
Línea 35:
Línea 19: <center>
<center>
<math>
<math>
- \mathrm{f}
+ X: \, E \longrightarrow R
- \left(
+
- \, x_i \,
+
- \right)
+
- \, = \,
+
- \mathrm{P}
+
- \left(
+
- \, X \, = \, x_i \,
+
- \right)
+
</math>
</math>
</center>
</center>
Línea 49:
Línea 25: <br/>
<br/>
- Por definición, deducimos que si
+ Al conjunto de valores de
<math>
<math>
- \left\{
+ R
- \, x_1, \, x_2, \ldots, \, x_n \,
+
- \right\}
+
</math>
</math>
- son los valores que puede tomar la variable
+ asignados a los elementos de
<math>
<math>
- X
+ E
</math>
</math>
- , entonces:
+ se le llama '''''recorrido''''' de la variable aleatoria y se representa por
-
+
- <br/>
+
-
+
- <center>
+
<math>
<math>
- \sum_{i \, = \, 1}^n \mathrm{f} \left( \, x_i \, \right) \, = \, \mathrm{f} \left( \,
+ X
- x_1 \, \right) \, + \, \mathrm{f} \left( \, x_2 \, \right) \, + \,
+ \left(
- \ldots \, + \, \mathrm{f} \left( \, x_n \, \right) \, = \, 1
+ \, E \,
+ \right)
</math>
</math>
- </center>
+ .
<br/>
<br/>
- ya que esta suma es, en realidad, la probabilidad del suceso seguro.
+ Una '''''variable aleatoria''''' es un valor numérico que corresponde al resultado de un
+ experimento aleatorio, como la suma de los puntos obtenidos al lanzar dos dados , el
+ número de lanzamientos de un dado hasta que aparece el cuatro, el número de personas que
+ suben en un determinado ascensor al mes , el tiempo de espera en la sala de un doctor.. .
<br/>
<br/>
- ===Ejemplo===
+ Las '''''variables aleatorias discretas''''' son aquellas que pueden tomar solamente un
+ número finitio o un número infinito numerable de valores.
<br/>
<br/>
- En el experimento de lanzar tres monedas al aire, la aplicación
+ A este nivel , las unicas variables aleatorias que consideraremos son aquellas que toman
- <math>
+ un número finito de valores. Un ejemplo de este tipo de variable aleatoria seria el
- X
+ resultado de lanzar un dado .
- </math>
+
- que asigna a cada resultado el numero de cruces obtenidas es una variable aleatoria. En este caso:
+
<br/>
<br/>
- <center>
+ Las '''''variables aleatorias continuas''''' son aquellas que pueden tomar cualquier
- <math>
+ valor en un intervalo de la recta real. Un ejemplo de este tipo de variable aleatoria
- \begin{array}[c]{cc}
+ seria la altura de una persona.
- \mathrm{f} \left( \, 0 \, \right) \, = \, \mathrm{P}
+
- \left(
+
- \, X \, = \, 0 \,
+
- \right)
+
- \, = \, \frac{1}{8} \qquad
+
- &
+
- \mathrm{f}
+
- \left(
+
- \, 1 \,
+
- \right)
+
- \, = \, \mathrm{P}
+
- \left(
+
- \, X \, = \, 1 \,
+
- \right)
+
- \, = \, \frac{3}{8}
+
- \qquad
+
- \\
+
- &
+
- \\
+
- \mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P}
+
- \left(
+
- \, X \, = \, 2 \,
+
- \right)
+
- \, = \, \frac{3}{8} \qquad
+
- &
+
- \mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P}
+
- \left(
+
- \, X \, = \, 3 \,
+
- \right)
+
- \, = \, \frac{1}{8} \qquad
+
- \end{array}
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
- Observa que
+
- <math>
+
- \mathrm{f} \left( \, 0 \, \right) \, + \, \mathrm{f} \left( \, 1 \, \right) \, + \,
+
- \mathrm{f} \left( \, 2 \, \right) \, + \, \mathrm{f} \left( \, 3 \, \right) \, = \, 1
+
- </math>
+
<br/>
<br/>
Línea 140:
Línea 73: <br/>
<br/>
- Dada una variable aleatoria discreta
+ Dada una variable aleatoria
<math>
<math>
X
X
</math>
</math>
- , su '''''función de distribución''''' es la aplicación que a cada valor de
+ , su '''''función de distribución''''' es la aplicación que a cada valor
<math>
<math>
- x_i
+ x
</math>
</math>
de la variable le asigna la probabilidad de que ésta tome valores menores o
de la variable le asigna la probabilidad de que ésta tome valores menores o
iguales que
iguales que
<math>
<math>
- x_i
+ x
</math>
</math>
, y la denotamos por:
, y la denotamos por:
Línea 159:
Línea 92: <center>
<center>
<math>
<math>
- \mathrm{F} \left( \, x_i \, \right) \, = \, \mathrm{P}
+ \mathrm{F} \left( \, x \, \right) \, = \, \mathrm{P}
\left(
\left(
- \, X \le x_i \,
+ \, X \le x \,
\right)
\right)
</math>
</math>
Línea 168:
Línea 101: <br/>
<br/>
- La función de distribución de cualquier variable aleatoria discreta tiene las siguentes
+ Como la función de distribución es una probabilidad,
- caracteristicas:
+
-
+
- <br/>
+
-
+
- 1. Al ser una probabilidad,
+
<math>
<math>
- 1 \ge \mathrm{F} \left( \, x_i \, \right) \ge 0
+ 1 \ge \mathrm{F} \left( \, x \, \right) \ge 0
</math>
</math>
.
.
Línea 181:
Línea 109: <br/>
<br/>
- 2.
+ [[Category:Matemáticas]]
- <math>
+
- \mathrm{F} \left( \, x \, \right)
+
- </math>
+
- es nula para todo valor de
+
- <math>
+
- x
+
- </math>
+
- menor que el menor valor de la variable aleatoria, y es igual a la unidad para
+
- todo valor de
+
- <math>
+
- x
+
- </math>
+
- mayor que el mayor valor de la variable.
+
- <br/>
+ %% }}}
-
+
- 3.
+
- <math>
+
- \mathrm{F} \left( \, x \, \right)
+
- </math>
+
- es creciente.
+
-
+
- <br/>
+
-
+
- 4.
+
- <math>
+
- \mathrm{F} \left( \, x \, \right)
+
- </math>
+
- es constante en cada intervalo
+
- <math>
+
- \left(
+
- \, x_i, \, x_{i \, + \, 1} \,
+
- \right)
+
- </math>
+
- , además es continua a la derecha de
+
- <math>
+
- x_i
+
- </math>
+
- y a la izquierda
+
- <math>
+
- x_{i \, + \, 1}
+
- </math>
+
- , y discontinua a la izquierda de
+
- <math>
+
- x_i
+
- </math>
+
- y a la derecha de
+
- <math>
+
- x_{i+1}
+
- </math>
+
- , para
+
- <math>
+
- i \, = \, 1, \, \ldots, \, n \, - \, 1
+
- </math>
+
-
+
-
+
- <br/>
+
-
+
- 5. Sea
+
- <math>
+
- x_j > x_i
+
- </math>
+
- , entonces
+
- <math>
+
- \mathrm{F}
+
- \left(
+
- \, x_j \,
+
- \right)
+
- \, - \,
+
- \mathrm{F}
+
- \left(
+
- \, x_i \,
+
- \right)
+
- \, = \,
+
- \mathrm{P}
+
- \left(
+
- \, x_j \ge X > x_i \,
+
- \right)
+
- </math>
+
-
+
- <br/>
+
-
+
- ==Distribución binomial==
+
-
+
- <br/>
+
-
+
- Supongamos que un experimento aleatorio tiene las siguientes caracteristicas:
+
-
+
- <br/>
+
-
+
- 1. En cada prueba del experimento sólo son posibles dos resultados: el suceso
+
- <math>
+
- A
+
- </math>
+
- , llamado ''exito'', y su contrario,
+
- <math>
+
- \bar{A}
+
- </math>
+
- , llamado ''fracaso''.
+
-
+
- <br/>
+
-
+
- 2. El resultado de cada prueba es independiente de los resultados obtenidos anteriormente.
+
-
+
- <br/>
+
-
+
- 3. La probabilidad de
+
- <math>
+
- A
+
- </math>
+
- , que denotamos por
+
- <math>
+
- p
+
- </math>
+
- , no varía de una prueba a otra.
+
-
+
- <br/>
+
-
+
- 4. En cada experimento se realizan
+
- <math>
+
- n
+
- </math>
+
- pruebas idénticas.
+
-
+
- <br/>
+
-
+
- Todo experimento aleatorio con estas características se dice que sigue el modelo de la
+
- distribución binomial.
+
-
+
- A la variable
+
- <math>
+
- X
+
- </math>
+
- , que representa el número de éxitos obtenidos en el experimento, se le
+
- llama '''''variable aleatoria binomial'''''.
+
-
+
- <br/>
+
-
+
- Al ser la variable aleatoria binomial una variable aleatoria discreta, tiene asociadas
+
- una función de probabilidad y una función de distribución.
+
-
+
- <br/>
+
-
+
- Existen varias maneras de obtener
+
- <math>
+
- r
+
- </math>
+
- exitos en las
+
- <math>
+
- n
+
- </math>
+
- pruebas. Supongamos que
+
- <math>
+
- n \, = \, 3
+
- </math>
+
- y calculemos la probabilidad del suceso
+
- <math>
+
- \left\{
+
- \, X \, = \, 2 \,
+
- \right\}
+
- </math>
+
- . Existen tres posibilidades de que ocurra
+
- <math>
+
- X \, = \, 2
+
- </math>
+
- :
+
-
+
- <br/>
+
-
+
- <center>
+
- <math>
+
- \begin{array}[c]{cc}
+
- 1^\circ: & \bar{A}AA
+
- \\
+
- 2^\circ: & A\bar{A}A
+
- \\
+
- 3^\circ: & AA\bar{A}
+
- \end{array}
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
- La diferencia entre estas tres posibilidades ( sucesos elementales ) es la prueba en que
+
- ocurre el fracaso. En el primer caso el fracaso ocurre en la primera prueba, en el
+
- segundo caso ocurre en la segunda y en el tercer caso ocurre en la tercera.
+
-
+
- <br/>
+
-
+
- Como estos sucesos son incompatibles, se tiene que:
+
-
+
- <br/>
+
-
+
- <center>
+
- <math>
+
- \mathrm{P}
+
- \left(
+
- \, X \, = \, 2 \,
+
- \right)
+
- \, = \, \mathrm{P}
+
- \left(
+
- \, \bar{A}AA \,
+
- \right)
+
- \, + \, \mathrm{P}
+
- \left(
+
- \, A\bar{A}A \,
+
- \right)
+
- \, + \, \mathrm{P}
+
- \left(
+
- \, AA\bar{A} \,
+
- \right)
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
-
+
- <math>
+
- \mathrm{P}
+
- \left(
+
- \, \bar{A}AA \,
+
- \right)
+
- \, = \, \mathrm{P}
+
- \left(
+
- \, A\bar{A}A \,
+
- \right)
+
- \, = \, \mathrm{P}
+
- \left(
+
- \, AA\bar{A} \,
+
- \right)
+
- \, = \, p^2 \cdot
+
- \left(
+
- \, 1 \, - \, p \,
+
- \right)
+
- </math>
+
- . Por ejemplo:
+
-
+
- <br/>
+
-
+
- <center>
+
- <math>
+
- \mathrm{P}
+
- \left(
+
- \, AA\bar{A}
+
- \right)
+
- \, = \, \mathrm{P} \left( \, A \, \right) \cdot \mathrm{P} \left( \, A \, \right)
+
- \cdot \mathrm{P} \left( \, \bar{A} \, \right)
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
- donde la ultima igualdad es cierta por que los resultados de las tres pruebas son
+
- independientes.
+
-
+
- <br/>
+
-
+
- Así
+
-
+
- <br/>
+
-
+
- <center>
+
- <math>
+
- \mathrm{P}
+
- \left(
+
- \, X \, = \, 2 \,
+
- \right)
+
- \, = \, 3 \cdot p^2 \cdot
+
- \left(
+
- \, 1 \, - \, p \,
+
- \right)
+
- </math>
+
- </center>
+
-
+
- <br/>
+
- En general:
+
-
+
- <br/>
+
-
+
- <center>
+
- <math>
+
- \mathrm{P}
+
- \left(
+
- \, X \, = \, r \,
+
- \right)
+
- \, = \,
+
- \left(
+
- \, { n \atop r }
+
- \right)
+
- \cdot p^r \cdot
+
- \left(
+
- \, 1 \, - \, p \,
+
- \right)
+
- ^
+
- \left(
+
- \, n \, - \, r \,
+
- \right)
+
- </math>
+
- </center>
+
-
+
- <br/>
+
-
+
- donde
+
- <math>
+
- \left(
+
- \, { n \atop r }
+
- \right)
+
- </math>
+
- es el numero de sucesos elementales que componen el suceso
+
- <math>
+
- \left\{
+
- \, X \, = \, r \,
+
- \right\}
+
- </math>
+
- ( estos sucesos elementales tienen en comun un mismo número de exitos y de
+
- fracasos y solo se diferencian en el orden en que ocurren los exitos y los fracasos ).
+
-
+
- <br/>
+
-
+
- <math>
+
- p^r \cdot
+
- \left(
+
- \, 1 \, - \, p \,
+
- \right)
+
- ^
+
- \left(
+
- \, n \, - \, r \,
+
- \right)
+
- </math>
+
- es la probabilidad de uno cualquiera de estos sucesos elementales.
+
-
+
- <br/>
+
-
+
- [[Category:Matemáticas]]
+
Revisión de 01:27 27 dic 2006
Definicion
Se llama variable aleatoria
Al conjunto de valores de
recorrido
Una variable aleatoria
Las variables aleatorias discretas
A este nivel, las unicas variables aleatorias que consideraremos son aquellas que toman
un número finito de valores. Un ejemplo de este tipo de variable aleatoria seria el
resultado de lanzar un dado.
Las variables aleatorias continuas
Función de distribución
Dada una variable aleatoria
función de distribución
Como la función de distribución es una probabilidad,
%% }}}
Los contenidos de
Wikillerato están disponibles bajo una
licencia de Creative Commons .
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
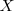 del espacio muestral
del espacio muestral
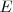 en un subconjunto de los numeros reales:
en un subconjunto de los numeros reales:
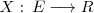
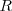 asignados a los elementos de
asignados a los elementos de
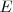 se le llama recorrido de la variable aleatoria y se representa por
se le llama recorrido de la variable aleatoria y se representa por
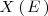 .
.
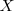 , su función de distribución es la aplicación que a cada valor
, su función de distribución es la aplicación que a cada valor
 de la variable le asigna la probabilidad de que ésta tome valores menores o
iguales que
de la variable le asigna la probabilidad de que ésta tome valores menores o
iguales que
 , y la denotamos por:
, y la denotamos por:
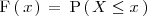
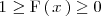 .
.



