La derivada como una tasa de variación instantánea

De Wikillerato

(Diferencias entre revisiones)

Fjmolina (Discutir | contribuciones)

Ir a las siguientes diferencias →

Revisión de 16:46 11 ene 2007

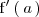La derivada de la función $\mathrm{f}$ en el punto $x \, = \, a$ , $\mathrm{f}^\prime \left( <pre> \, a \, </pre> \right)$ , si existe, es el valor del limite:

$\lim_{h \to 0} \frac{\mathrm{f}\left( \, a \, + \, h \, \right) \, - \, <pre> \mathrm{f} \left( \, a \, \right)}{h} </pre> $ .

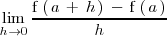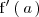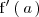Si $\mathrm{f}^\prime \left( <pre> \, a \, </pre> \right)$ es un número real, la función $\mathrm{f}$ es derivable en $x \, = \, a$ . Si $\mathrm{f}^\prime \left( <pre> \, a \, </pre> \right)$ no es un número real o el límite no existe, la función $\mathrm{f}$ no es derivable en dicho punto.

Ejemplo

Calculemos la derivada de 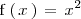$\mathrm{f} \left( <pre> \, x \, </pre> \right) \, = \, x^2$ en $x \, = \, 2$ :

$\mathrm{f}^\prime \left( <pre> \, 2 \, </pre> \right) \, = \, \lim_{h \to 0} \frac{\mathrm{f}\left( \, 2 \, + \, h \, \right) \, - \, <pre> \mathrm{f} \left( \, 2 \, \right)}{h} \, = \, \lim_{h \to 0} \frac </pre> {\left( \, 2 \, + \, h \, \right)^2 \, - \, 2^2}{h} \, = \,$

$\, = \, \lim_{h \to 0} \frac {\left( \, 4 \, + \, 4h \, + \, h^2 \, \right) \, - \, 4}{h} \, = \, \lim_{h \to 0} \frac {4h \, + \, h^2}{h} \, = \, \lim_{h \to 0} \left( <pre> \, h \, + 4 \, \, \right) \, = \, 4 </pre> $

%% }}} %% {{{ =

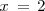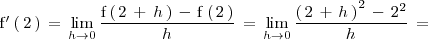
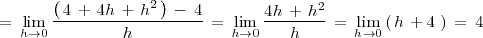
Tasa de variación media

Supongamos que un coche formula uno se mueve en una carretera totalmente recta. A distintas distancias de la salida se registran los tiempos de paso, obteniendose la siguiente tabla:

En este caso, la posición, $y$ , se puede ver como una función, $\mathrm{f}$ , del tiempo, $x$ . Es decir:

$y \, = \, \mathrm{f} \left( \, x \, \right)$

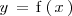
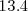La tasa de variación media de la posición en el intervalo de tiempo desde el instante $9$ al instante $13.4$ es:

[Unparseable or potentially dangerous latex formula. Error 3 ]

En general, la tasa de variación media de la función $\mathrm{f}$ en $\left[ <pre> \, a, \, b \, </pre> \right]$ se define como el cociente:

$\frac{\mathrm{f} \left( \, b \, \right) \, - \, \mathrm{f} \left( \, a \, <pre> \right)}{b \, - \, a} </pre> $

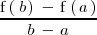
Tasa de variación instantánea

La tasa de variación instantánea de la función $f$ en el punto $x \, = \, a$ se obtiene haciendo tender $b$ a $a$ en la tasa de variación media' de la función $f$ en el intervalo $\left[ <pre> \, a, \, b \, </pre> \right]$ . Por tanto, la tasa de variación instantánea de la función $f$ en el punto $x \, = \, a$ es