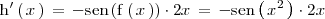Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Función derivada de la composición de funciones

De Wikillerato

(Diferencias entre revisiones)
Línea 81: Línea 81:
<center>
<center>
<math>
<math>
-
\mathrm{f} \left( \, x \, \right) \, = \, x^2
+
\left\{
-
</math>
+
\begin{array}[c]{rcl}
-
</center>
+
\mathrm{f} \left( \, x \, \right) \, & = & \, x^2
-
 
+
\\
-
<center>
+
\mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right)
-
<math>
+
\end{array}
-
\mathrm{g} \left( \, x \, \right) \, = \, \cos \left( \, x \, \right)
+
\right.
</math>
</math>
</center>
</center>
Línea 127: Línea 127:
<center>
<center>
<math>
<math>
-
\mathrm{f}^\prime \left( \, x \, \right) \, = 2x \,
+
\left\{
-
</math>
+
\begin{array}[c]{rcl}
-
 
+
\mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x
-
<br/>
+
\\
-
 
+
\mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right)
-
<math>
+
\end{array}
-
\mathrm{g}^\prime \left( \, x \, \right) \, = -\mathrm{sen} \left( \, x \, \right)
+
\right.
</math>
</math>
</center>
</center>

Revisión de 16:51 12 ene 2007

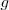El componer dos funciones   \mathrm{f}   y   \mathrm{g}   consiste en aplicar   g   al resultado de calcular 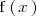  \mathrm{f} \left( \, x \, \right) , es decir:


R \stackrel{\mathrm{f}}{\longrightarrow} R \stackrel{\mathrm{g}}{\longrightarrow} R


x \longrightarrow \mathrm{f} \left( \, x \, \right) \longrightarrow \mathrm{g} \left( \mathrm{f} \left( \, x \, \right) \right)


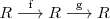
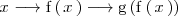
La derivada de 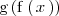  \mathrm{g} \left( \mathrm{f} \left( \, x \, \right) \right)   viene dada por la fórmula: 


[Unparseable or potentially dangerous latex formula. Error 3 ]


resultado que se conoce como regla de la cadena.


Ejemplo


Calculemos la derivada de


\mathrm{h} \left( \, x \, \right) \, = \, \cos \left( \, x^2 \, \right)


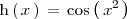
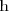  \mathrm{h}   es la composición de dos funciones:


\left\{ </p> <pre> \begin{array}[c]{rcl} \mathrm{f} \left( \, x \, \right) \, & = & \, x^2 \\ \mathrm{g} \left( \, x \, \right) \, & = & \, \cos \left( \, x \, \right) \end{array} </pre> <p>\right.


Es decir


\mathrm{h} \left( \, x \, \right) \, = \, \mathrm{g} \left( \, \mathrm{f} \left( \, x \, \right) \right)


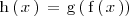
Para derivar 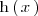  \mathrm{h} \left( \, x \, \right)   utilizamos la regla de la cadena:


</p> <pre> \mathrm{h}^\prime \left( \, x \, \right) \, = \, \mathrm{g}^\prime \left( \, \mathrm{f} \left( \, x \, \right) \right) \cdot \mathrm{f}^\prime \left( \, x \, \right) </pre> <p>


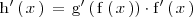
Como


\left\{ </p> <pre> \begin{array}[c]{rcl} \mathrm{f}^\prime \left( \, x \, \right) \, & = & \, 2x \\ \mathrm{g}^\prime \left( \, x \, \right) \, & = & \, -\mathrm{sen} \left( \, x \, \right) \end{array} </pre> <p>\right.


se tiene que


\mathrm{h}^\prime \left( \, x \, \right) \, = \, -\mathrm{sen} \left( </p> <pre> \mathrm{f} \left( \, x \, \right) \right) \cdot 2x \, = \, -\mathrm{sen} \left( \, x^2 \, \right) \cdot 2x </pre> <p>


Obtenido de "http://wikillerato.org/Funci%C3%B3n_derivada_de_la_composici%C3%B3n_de_funciones.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.