Método deductivo de las ciencias formales: Matemáticas.
De Wikillerato
| Línea 13: | Línea 13: | ||
Este nuevo enfoque de las Matemáticas, concibe a esta ciencia como <b>un sistema formal axiomático</b>. Si conseguimos entender estas palabras, habremos comprendido la estructura de las Matemáticas. | Este nuevo enfoque de las Matemáticas, concibe a esta ciencia como <b>un sistema formal axiomático</b>. Si conseguimos entender estas palabras, habremos comprendido la estructura de las Matemáticas. | ||
| - | Un sistema formal axiomático, está constituido por un conjunto de proposiciones llamadas <b>[[tesis]]</b> del sistema, de las que unas son los <b>[[Los axiomas|axiomas]]</b> y otras los <b>[[ | + | Un sistema formal axiomático, está constituido por un conjunto de proposiciones llamadas <b>[[tesis]]</b> del sistema, de las que unas son los <b>[[Método deductivo de las ciencias formales: Matemáticas.#Los axiomas|axiomas]]</b> y otras los <b>[[Método deductivo de las ciencias formales: Matemáticas.#Los teoremas|teoremas]]</b>. |
| Línea 24: | Línea 24: | ||
Para hacernos una idea adecuada del sistema formal axiomático, pondremos como ejemplo, el del <b>juego de ajedrez</b>. Los axiomas son las reglas del juego, de las que no se pueden salir los jugadores, y, por tanto, en los sistemas formales axiomáticos, los axiomas deben quedar bien establecidos para que se puedan deducir los teoremas con ausencia de contradicción. | Para hacernos una idea adecuada del sistema formal axiomático, pondremos como ejemplo, el del <b>juego de ajedrez</b>. Los axiomas son las reglas del juego, de las que no se pueden salir los jugadores, y, por tanto, en los sistemas formales axiomáticos, los axiomas deben quedar bien establecidos para que se puedan deducir los teoremas con ausencia de contradicción. | ||
| + | |||
| + | <h4>Los teoremas</h4> | ||
| + | |||
| + | Son las proposiciones o tesis del sistema formal axiomático que se demuestran a partir de los [[Método deductivo de las ciencias formales: Matemáticas.#Los axiomas|axiomas]], o a partir de otros teoremas ya demostrados. | ||
| + | |||
| + | <h5>Estructura de un sistema formal axiomático</h5> | ||
| + | <li>Parte morfológica</li> | ||
| + | #Un conjunto de componentes primitivos. | ||
| + | #Un conjunto de operaciones relativas a tales componentes. | ||
| + | #Un conjunto de reglas de formación expresivas de cómo a partir de los componentes primitivos se pueden construir nuevos componentes llamados derivados. | ||
| + | <li>Parte axiomática</li> | ||
| + | #Un conjunto de axiomas. | ||
| + | #Un conjunto de definiciones. | ||
| + | #Un conjunto de reglas o criterios de deducción. | ||
| + | #Un conjunto de teoremas demostrados, que se basan en los tres conjuntos anteriores. | ||
| + | |||
| + | Lo que se refiere a la parte morfológica, lo hemos estudiado en la [[Lógica proposicional]]. En cuanto a la parte axiomática, se han formulado diferentes grupos de axiomas como los de [[Lukasiewicz]], los de [[Frege]] – [[Lukasiewicz]], y los de [[Hilbert]] – [[Ackermann]], que pasamos a exponer. | ||
| + | |||
| + | |||
| + | <h5>Axiomas</h5> | ||
| + | <li><b>A 1:</b> <math>( p \lor p ) \to p</math></li> | ||
| + | <li><b>A 2:</b> <math> p \to (p \lor q)</math></li> | ||
| + | <li><b>A 3:</b> <math>(p \lor q) \to q \lor p</math></li> | ||
| + | <li><b>A 4:</b> <math>(p \to q) \to [(r \lor p) \to (r \lor q)] </math> </li> | ||
| + | |||
| + | |||
| + | <h5>Definiciones</h5> | ||
| + | |||
| + | Tienen como fin establecer el significado de los operadores no primitivos o derivados. | ||
| + | <li><b>Df, 1:</b> <math>p \to q = df \bar{p} v q</math></li> | ||
| + | <li><b>Df, 2:</b> <math>p \land q = df \overline {\bar p \lor \bar q}</math></li> | ||
| + | <li><b>Df. 3:</b> <math>p \underline{\lor } q = df \overline { p \to q} \lor \overline {(q \to p)}</math></li> | ||
| + | <li><b>Df. 4:</b> <math>p \leftrightarrow q = df (p \to q) \land (q \to p)</math></li> | ||
| + | |||
| + | |||
| + | <h5>Criterios de deducción</h5> | ||
| + | <li>D 1: A 1, A 2, A 3, A 4 son tesis.</li> | ||
| + | <li>D 2: Si <math>p</math> es una tesis y si <math>p \to q</math> es una tesis, entonces <math>q</math> es una tesis (modus ponendo ponens).</li> | ||
| + | <li>D 3: Si una expresión lógica es una tesis y sustituimos en ella una proposición atómica por otra cualquiera, el resultado es una tesis.</li> | ||
| + | <li>D 4: Si <math>p \to q</math> es una tesis, y si <math>q \to p</math> es una tesis, entonces <math>q \to r</math> es una tesis.</li> | ||
| + | <li>D 5: Nada es tesis si no es mediante los criterios: D 1, D 2, D 3 y D 4.</li> | ||
| + | |||
| + | A partir de estos axiomas, definiciones y criterios de deducción se pueden ir demostrando los teoremas de la [[lógica proposicional]]. Por ejemplo: | ||
| + | <li>A partir de A 2, D 1, D 3, se obtiene: <math>p \to ( p \lor p)</math> <b> T1.</b></li> | ||
| + | <li>A partir de A 1, T 1, D 1, D 4: <math>p \to p</math> <b> T2.</b></li> | ||
| + | <li>A partir de T 2, Df 1: <math>\overline {p} \lor p</math> <b> T3.</b></li> | ||
| + | <li>A partir de A 3, D 1, D 3 : <math>(\overline{p} \lor p) \to ( p \lor \overline {p})</math> <b> T4.</b></li> | ||
| + | <li>A partir de T 3, T 4, D 2 : <math>(p \lor \overline {p})</math> <b> T5.</b></li> | ||
Revisión de 11:57 30 may 2007
Tabla de contenidos |
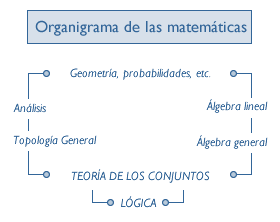
Las Matemáticas
No es tarea fácil definir las Matemáticas debido al gran progreso que han experimentado en los últimos siglos. Se ha venido afirmando que las Matemáticas estudian el número y la extensión, pero esta definición ha quedado anticuada. Vamos a exponer un esquema muy simplificado de las distintas partes de esta ciencia para hacernos una idea de su contenido:
En los fundamentos de las Matemáticas, está la teoría de los conjuntos y la Lógica.
Esta fundamentación ha dado origen a la matemática moderna que ha supuesto una revolución. Esta revolución surgió para dar al conjunto de los conocimientos matemáticos una mayor consistencia y coherencia. Tal fue la intención de sus creadores, Hilbert, Cantor y Russell. También fueron importantes las aportaciones de los matemáticos franceses reunidos bajo el nombre de Nicolás Bourbaki. Para todos ellos era más importante enunciar y demostrar con el máximo rigor los principales teoremas de las Matemáticas que descubrir otros nuevos.
Este nuevo enfoque de las Matemáticas, concibe a esta ciencia como un sistema formal axiomático. Si conseguimos entender estas palabras, habremos comprendido la estructura de las Matemáticas.
Un sistema formal axiomático, está constituido por un conjunto de proposiciones llamadas tesis del sistema, de las que unas son los axiomas y otras los teoremas.
Los axiomas
Son las proposiciones básicas del sistema. Axioma viene del griego αξιωματα que significa dignidades. Son las proposiciones más dignas, las primeras. Así las bautizó Euclides en sus Elementos. Antiguamente estos axiomas eran evidentes; es decir, su verdad se imponía inmediatamente a la mente. Son los llamados axiomas materiales.
En la actualidad, sin embargo, los axiomas se enuncian como axiomas formales, como proposiciones cuya verdad no se plantea como problema, pero que se establecen como fundamento de todas las demás proposiciones del sistema formal axiomático.
Para hacernos una idea adecuada del sistema formal axiomático, pondremos como ejemplo, el del juego de ajedrez. Los axiomas son las reglas del juego, de las que no se pueden salir los jugadores, y, por tanto, en los sistemas formales axiomáticos, los axiomas deben quedar bien establecidos para que se puedan deducir los teoremas con ausencia de contradicción.
Los teoremas
Son las proposiciones o tesis del sistema formal axiomático que se demuestran a partir de los axiomas, o a partir de otros teoremas ya demostrados.
Estructura de un sistema formal axiomático
- Un conjunto de componentes primitivos.
- Un conjunto de operaciones relativas a tales componentes.
- Un conjunto de reglas de formación expresivas de cómo a partir de los componentes primitivos se pueden construir nuevos componentes llamados derivados.
- Un conjunto de axiomas.
- Un conjunto de definiciones.
- Un conjunto de reglas o criterios de deducción.
- Un conjunto de teoremas demostrados, que se basan en los tres conjuntos anteriores.
Axiomas
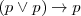 </li>
</li>
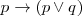 </li>
</li>
 </li>
</li>
![(p \to q) \to [(r \lor p) \to (r \lor q)] (p \to q) \to [(r \lor p) \to (r \lor q)]](/images/math/math-2fb5a3e73dc79b19d27895f072d3230d.png) </li>
</li>
Definiciones
Tienen como fin establecer el significado de los operadores no primitivos o derivados.
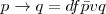 </li>
</li>
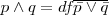 </li>
</li>
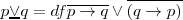 </li>
</li>
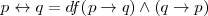 </li>
</li>
Criterios de deducción
 es una tesis y si
es una tesis y si 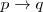 es una tesis, entonces
es una tesis, entonces 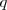 es una tesis (modus ponendo ponens).</li>
es una tesis (modus ponendo ponens).</li>
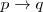 es una tesis, y si
es una tesis, y si 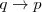 es una tesis, entonces
es una tesis, entonces 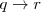 es una tesis.</li>
es una tesis.</li>
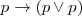 T1.</li>
T1.</li>
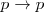 T2.</li>
T2.</li>
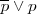 T3.</li>
T3.</li>
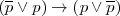 T4.</li>
T4.</li>
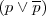 T5.</li>
Tweet
T5.</li>
Tweet