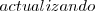Ayuda:Fórmulas Matemáticas
De Wikillerato
(Diferencias entre revisiones)
| Línea 240: | Línea 240: | ||
<table style="border: 1px solid rgb(170, 170, 170); margin: 1em 1em 1em 0pt; background: rgb(249, 249, 249) none repeat scroll 0%;border-collapse: collapse;" border="2" cellpadding="4" cellspacing="0"> | <table style="border: 1px solid rgb(170, 170, 170); margin: 1em 1em 1em 0pt; background: rgb(249, 249, 249) none repeat scroll 0%;border-collapse: collapse;" border="2" cellpadding="4" cellspacing="0"> | ||
<tr> | <tr> | ||
| - | <th | + | <th> </th> |
| - | <th | + | <th>Sintaxis</th> |
| - | <th | + | <th>Cómo se verá</th> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Superíndice</td> | <td>Superíndice</td> | ||
<td><code>a^2</code></td> | <td><code>a^2</code></td> | ||
| - | |||
<td><math> a^2 </math></td> | <td><math> a^2 </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td> | + | <td>Subíndice</td> |
<td><code>a_2</code></td> | <td><code>a_2</code></td> | ||
| - | |||
<td><math> a_2 </math></td> | <td><math> a_2 </math></td> | ||
</tr> | </tr> | ||
| Línea 263: | Línea 257: | ||
<td rowspan="2">Agrupar</td> | <td rowspan="2">Agrupar</td> | ||
<td><code>a^{2+2}</code></td> | <td><code>a^{2+2}</code></td> | ||
| - | |||
<td><math> a^{2+2} </math></td> | <td><math> a^{2+2} </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><code>a_{i,j}</code></td> | <td><code>a_{i,j}</code></td> | ||
| - | |||
<td><math> a_{i,j} </math></td> | <td><math> a_{i,j} </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td>Combinar | + | <td>Combinar superindice y subíndice</td> |
<td><code>x_2^3</code></td> | <td><code>x_2^3</code></td> | ||
| - | <td | + | <td><math> x_2^3 </math></td> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td><code>{ | + | <td rowspan="2">Superíndices y subíndices, anteriores, posteriores, arriba y abajo</td> |
| - | <td | + | <td><code>\sideset {_1^2} {_3^4} \prod_a^b</code></td> |
| + | <td><math> \sideset {_1^2} {_3^4} \prod_a^b </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | + | <td><code>{}_1^2 \! \Omega_3^4</code></td> | |
| - | <td><code> | + | <td><math> {}_1^2 \! \Omega_3^4 </math></td> |
| - | <td | + | |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td><code>\ | + | <td rowspan="3">Apilar</td> |
| - | <td | + | <td><code>\overset { \alpha} { \omega}</code></td> |
| + | <td><math> \overset { \alpha} { \omega} </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td><code>\overset{\alpha}{\underset{\gamma}{\omega}}</code></td> | + | <td><code>\overset { \alpha} { \underset { \gamma} { \omega}}</code></td> |
| - | <td | + | <td><math> \overset { \alpha} { \underset { \gamma} { \omega}} </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td><code>\stackrel{\alpha}{\omega}</code></td> | + | <td><code>\stackrel { \alpha} { \omega}</code></td> |
| - | <td | + | <td><math> \stackrel { \alpha} { \omega} </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td>Derivadas | + | <td>Derivadas</td> |
<td><code>x', y'', f', f''</code></td> | <td><code>x', y'', f', f''</code></td> | ||
| - | <td | + | <td><math> x', y'', f', f'' </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td rowspan="3">Subrayado, | + | <td rowspan="3">Subrayado, línea superior, vectores</td> |
<td><code>\hat a \ \bar b \ \vec c</code></td> | <td><code>\hat a \ \bar b \ \vec c</code></td> | ||
| - | <td | + | <td><math> \hat a \ \bar b \ \vec c </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td><code>\overrightarrow{a b} | + | <td><code>\overrightarrow {a b} \overleftarrow {c d} \widehat {d e f}</code></td> |
| - | <td | + | <td><math> \overrightarrow {a b} \overleftarrow {c d} \widehat {d e f} </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td><code>\overline{g h i} | + | <td><code>\overline {g h i} \underline {j k l}</code></td> |
| - | <td | + | <td><math> \overline {g h i} \underline {j k l} </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Flechas</td> | <td>Flechas</td> | ||
| - | <td><code>A \xleftarrow{n+\mu-1} B \xrightarrow[T]{n\pm i-1} C</code></td> | + | <td><code>A \xleftarrow {n+ \mu-1} B \xrightarrow[T] {n \pm i-1} C</code></td> |
| - | <td | + | <td><math> A \xleftarrow {n+ \mu-1} B \xrightarrow[T] {n \pm i-1} C </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Llaves superiores</td> | <td>Llaves superiores</td> | ||
| - | <td><code>\overbrace{ 1+2+\cdots+100 }^{5050}</code></td> | + | <td><code>\overbrace{ 1+2+ \cdots+100 } ^ {5050}</code></td> |
| - | <td | + | <td><math> \overbrace{ 1+2+ \cdots+100 } ^ {5050} </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Llaves inferiores</td> | <td>Llaves inferiores</td> | ||
| - | <td><code>\underbrace{ a+b+\cdots+z }_{26}</code></td> | + | <td><code>\underbrace { a+b+ \cdots+z }_{26}</code></td> |
| - | <td | + | <td><math> \underbrace { a+b+ \cdots+z }_{26} </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Sumatorios</td> | <td>Sumatorios</td> | ||
<td><code>\sum_{k=1}^N k^2</code></td> | <td><code>\sum_{k=1}^N k^2</code></td> | ||
| - | <td | + | <td><math> \sum_{k=1}^N k^2 </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Productorio</td> | <td>Productorio</td> | ||
<td><code>\prod_{i=1}^N x_i</code></td> | <td><code>\prod_{i=1}^N x_i</code></td> | ||
| - | <td | + | <td><math> \prod_{i=1}^N x_i </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td> | + | <td>Coproducto</td> |
<td><code>\coprod_{i=1}^N x_i</code></td> | <td><code>\coprod_{i=1}^N x_i</code></td> | ||
| - | <td | + | <td><math> \coprod_{i=1}^N x_i </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td> | + | <td>Límite</td> |
<td><code>\lim_{n \to \infty}x_n</code></td> | <td><code>\lim_{n \to \infty}x_n</code></td> | ||
| - | <td | + | <td><math> \lim_{n \to \infty}x_n </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Integral</td> | <td>Integral</td> | ||
<td><code>\int_{-N}^{N} e^x\, dx</code></td> | <td><code>\int_{-N}^{N} e^x\, dx</code></td> | ||
| - | <td | + | <td ><math>\int_{-N}^{N} e^x\, dx</math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Integral doble</td> | <td>Integral doble</td> | ||
<td><code>\iint_{D}^{W} \, dx\,dy</code></td> | <td><code>\iint_{D}^{W} \, dx\,dy</code></td> | ||
| - | <td | + | <td><math> \iint_{D}^{W} \, dx\,dy </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Integral triple</td> | <td>Integral triple</td> | ||
<td><code>\iiint_{E}^{V} \, dx\,dy\,dz</code></td> | <td><code>\iiint_{E}^{V} \, dx\,dy\,dz</code></td> | ||
| - | <td | + | <td><math> \iiint_{E}^{V} \, dx\,dy\,dz </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Integral de línea</td> | <td>Integral de línea</td> | ||
<td><code>\oint_{C} x^3\, dx + 4y^2\, dy</code></td> | <td><code>\oint_{C} x^3\, dx + 4y^2\, dy</code></td> | ||
| - | <td | + | <td><math> \oint_{C} x^3\, dx + 4y^2\, dy </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Intersecciones</td> | <td>Intersecciones</td> | ||
<td><code>\bigcap_1^{n} p</code></td> | <td><code>\bigcap_1^{n} p</code></td> | ||
| - | <td | + | <td><math> \bigcap_1^{n} p </math></td> |
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>Uniones</td> | <td>Uniones</td> | ||
<td><code>\bigcup_1^{k} p</code></td> | <td><code>\bigcup_1^{k} p</code></td> | ||
| - | <td | + | <td><math> \bigcup_1^{k} p </math></td> |
</tr> | </tr> | ||
</table> | </table> | ||
Revisión de 12:14 6 nov 2007
Ayuda A continuación ofrecemos un cuadro de referencia con nociones básicas y ejemplos que sirven de ayuda para escribir fórmulas utilizando el código LaTeX.
Tabla de contenidos |
Básicos
| Acentos | |
|---|---|
\acute{a} \grave{a} \hat{a} \tilde{a} \breve{a} |
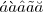 |
\check{a} \bar{a} \ddot{a} \dot{a} |
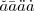 |
| Funciones estándar | |
\sin a \cos b \tan c |
 |
\sec d \csc e \cot f |
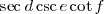 |
\arcsin h \arccos i \arctan j |
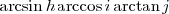 |
\sinh k \cosh l \tanh m \coth n |
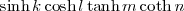 |
\lim u \limsup v \liminf w \min x \max y |
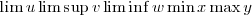 |
\inf z \sup a \exp b \ln c \lg d \log e \log_{10} f \ker g |
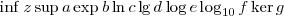 |
| Derivadas | |
\nabla \partial x dx \dot x \ddot y |
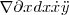 |
| Conjuntos | |
\forall \exists \emptyset \varnothing |
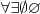 |
\in \ni \notin \subset \subseteq \supset \supseteq |
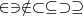 |
\cap \bigcap \cup \bigcup \biguplus \setminus \smallsetminus |
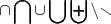 |
\sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup |
 |
| Operadores | |
+ \oplus \bigoplus \pm \mp - |
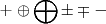 |
\times \otimes \bigotimes \cdot \circ \bullet \bigodot |
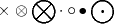 |
\star * / \div \frac{1}{2} |
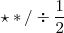 |
| Lógica | |
\land \wedge \bigwedge \bar{q} \to p |
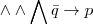 |
\lor \vee \bigvee \lnot \neg q \And |
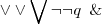 |
| Raíces | |
\sqrt{2} \sqrt[n]{x} |
![\sqrt{2} \sqrt[n]{x} \sqrt{2} \sqrt[n]{x}](/images/math/math-0aed309c6c6fb7ceae2817c32bc29384.png) |
| Relaciones | |
\sim \approx \simeq \cong |
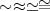 |
\le < \ll \gg \ge > \equiv \not\equiv \ne \mbox{or} \neq \propto |
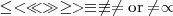 |
| Geometría | |
\Diamond \Box \triangle \angle \perp \mid \nmid \| 45^\circ |
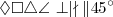 |
| Flechas | |
\leftarrow \gets \rightarrow \to \not\to \leftrightarrow \longleftarrow \longrightarrow |
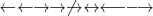 |
\uparrow \downarrow \updownarrow \rightharpoonup \rightharpoondown \leftharpoonup \leftharpoondown \upharpoonleft |
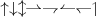 |
\upharpoonright \downharpoonleft \downharpoonright \rightleftharpoons \Leftarrow \Rightarrow \Leftrightarrow \Longleftarrow |
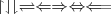 |
\Longrightarrow \Uparrow \Downarrow \Updownarrow |
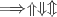 |
\nLeftrightarrow \longleftrightarrow |
 |
| Especial | |
\eth \S \P \% \dagger \ddagger \ldots \cdots |
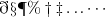 |
\smile \frown \wr \triangleleft \triangleright \infty \bot \top |
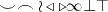 |
\vdash \vDash \Vdash \models \lVert \rVert \imath \hbar |
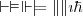 |
| Otros | |
\vartriangle \triangledown \lozenge \circledS \measuredangle \nexists \Bbbk \backprime \blacktriangle \blacktriangledown |
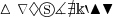 |
\blacksquare \blacklozenge \bigstar \sphericalangle \diagup \diagdown \dotplus \Cap \Cup \barwedge |
 |
\veebar \doublebarwedge \boxminus \boxtimes \boxdot \boxplus \divideontimes \ltimes \rtimes \leftthreetimes |
 |
\rightthreetimes \curlywedge \curlyvee \circleddash \circledast \circledcirc \centerdot \intercal \leqq \leqslant |
 |
\eqslantless \lessapprox \approxeq \lessdot \lll \lessgtr \lesseqgtr \lesseqqgtr \doteqdot |
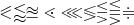 |
\fallingdotseq \backsim \backsimeq \subseteqq \Subset \preccurlyeq \curlyeqprec \precsim \precapprox |
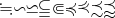 |
\Vvdash \bumpeq \Bumpeq \geqq \geqslant \eqslantgtr \gtrsim \gtrapprox \eqsim \gtrdot |
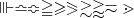 |
\ggg \gtrless \gtreqless \gtreqqless \eqcirc \circeq \triangleq \thicksim \thickapprox \supseteqq |
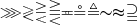 |
\Supset \succcurlyeq \curlyeqsucc \succsim \succapprox \vartriangleright \shortmid \shortparallel \between \pitchfork |
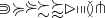 |
\varpropto \blacktriangleleft \therefore \backepsilon \blacktriangleright \because \nleqslant \nleqq \lneq \lneqq |
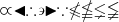 |
\lvertneqq \lnsim \lnapprox \nprec \npreceq \precneqq \precnsim \precnapprox \nsim \nshortmid |
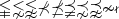 |
\nvdash \nVdash \ntriangleleft \ntrianglelefteq \nsubseteq \nsubseteqq \ngtr |
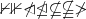 |
\ngeqslant \ngeqq \gneq \gneqq \gvertneqq \gnsim \gnapprox \nsucc \nsucceq \succneqq |
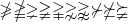 |
\succnsim \succnapprox \ncong \nshortparallel \nparallel \nvDash \nVDash \ntriangleright \ntrianglerighteq \nsupseteq |
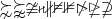 |
\nsupseteqq \varsupsetneq \supsetneqq \varsupsetneqq |
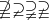 |
Subíndices, superíndices, integrales
| Sintaxis | Cómo se verá | |
|---|---|---|
| Superíndice | a^2 |
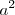 |
| Subíndice | a_2 |
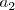 |
| Agrupar | a^{2+2} |
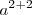 |
a_{i,j} |
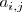 |
|
| Combinar superindice y subíndice | x_2^3 |
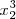 |
| Superíndices y subíndices, anteriores, posteriores, arriba y abajo | \sideset {_1^2} {_3^4} \prod_a^b |
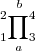 |
{}_1^2 \! \Omega_3^4 |
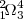 |
|
| Apilar | \overset { \alpha} { \omega} |
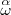 |
\overset { \alpha} { \underset { \gamma} { \omega}} |
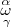 |
|
\stackrel { \alpha} { \omega} |
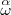 |
|
| Derivadas | x', y, f', f |
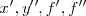 |
| Subrayado, línea superior, vectores | \hat a \ \bar b \ \vec c |
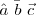 |
\overrightarrow {a b} \overleftarrow {c d} \widehat {d e f} |
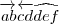 |
|
\overline {g h i} \underline {j k l} |
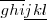 |
|
| Flechas | A \xleftarrow {n+ \mu-1} B \xrightarrow[T] {n \pm i-1} C |
![A \xleftarrow {n+ \mu-1} B \xrightarrow[T] {n \pm i-1} C A \xleftarrow {n+ \mu-1} B \xrightarrow[T] {n \pm i-1} C](/images/math/math-4b1c51a2068786607a20bbdb3abe502e.png) |
| Llaves superiores | \overbrace{ 1+2+ \cdots+100 } ^ {5050} |
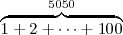 |
| Llaves inferiores | \underbrace { a+b+ \cdots+z }_{26} |
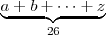 |
| Sumatorios | \sum_{k=1}^N k^2 |
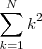 |
| Productorio | \prod_{i=1}^N x_i |
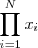 |
| Coproducto | \coprod_{i=1}^N x_i |
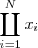 |
| Límite | \lim_{n \to \infty}x_n |
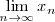 |
| Integral | \int_{-N}^{N} e^x\, dx |
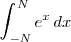 |
| Integral doble | \iint_{D}^{W} \, dx\,dy |
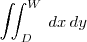 |
| Integral triple | \iiint_{E}^{V} \, dx\,dy\,dz |
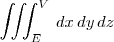 |
| Integral de línea | \oint_{C} x^3\, dx + 4y^2\, dy |
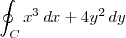 |
| Intersecciones | \bigcap_1^{n} p |
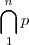 |
| Uniones | \bigcup_1^{k} p |
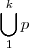 |
Fracciones, matrices, multilíneas
Alfabetos
Añadiendo paréntesis a grandes expresiones
Espaciado
Colores
Ejemplos