Propagación de una perturbación en un medio
De Wikillerato
| Línea 1: | Línea 1: | ||
El movimiento ondulatorio es la propagación de una perturbación en un medio elástico producida en uno cualquiera de sus puntos. El movimiento ondulatorio transporta o propaga energía sin que haya traslación de los puntos del medio. | El movimiento ondulatorio es la propagación de una perturbación en un medio elástico producida en uno cualquiera de sus puntos. El movimiento ondulatorio transporta o propaga energía sin que haya traslación de los puntos del medio. | ||
| - | <span style="text-decoration:underline">Observaciones</span> | + | <span style="text-decoration:underline">'''Observaciones'''</span> |
| - | '''a)'''Perturbación propagándose a lo largo de una cuerda | + | '''a)''' Perturbación propagándose a lo largo de una cuerda |
Imaginemos una cuerda mantenida horizontal a la que propinamos una sacudida en uno de sus extremos. Observamos que la deformación que hemos provocado se desplaza rápidamente a lo largo de la cuerda. | Imaginemos una cuerda mantenida horizontal a la que propinamos una sacudida en uno de sus extremos. Observamos que la deformación que hemos provocado se desplaza rápidamente a lo largo de la cuerda. | ||
| Línea 24: | Línea 24: | ||
La onda es '''unidimensional''' puesto que se propaga en una sola dirección. | La onda es '''unidimensional''' puesto que se propaga en una sola dirección. | ||
| + | |||
| + | '''b)''' Perturbación sobre la superficie de un líquido. | ||
| + | |||
| + | Podemos rellenar de agua una bandeja poco profunda colocando en un lugar cualquiera de su superficie un tapón de corcho. | ||
| + | |||
| + | Si tocamos ligeramente con un punzón, se observará un círculo que irá haciéndose mayor. Cuando alcance la posición del corcho, se observará que éste realizará una oscilación vertical, pero no se trasladará sobre la superficie del agua. El movimiento del corcho nos pondrá en evidencia el movimiento de cada punto de la superficie del agua cuando le llega la perturbación. La onda generada será transversal y '''bidimensional''' puesto que se propaga en un plano. | ||
| + | |||
| + | '''c)''' Deformación que se propaga a lo largo de un resorte. | ||
| + | |||
| + | Sobre un resorte que hemos sujetado por sus extremos, manteniéndolo horizontal en la medida de lo posible, realizamos una deformación comprimiendo una parte del mismo. Inmediatamente después, soltamos, se observa que esa compresión se va propagando a lo largo del resorte. | ||
| + | |||
| + | El mismo efecto se observa si en lugar de comprimir las espiras, las separamos (decimos que realizamos una depresión o expansión) | ||
| + | |||
| + | Podemos hacer una representación esquemática de las espiras. | ||
| + | |||
| + | Consideremos que las espiras en ningún momento se yuxtaponen. Partimos de la posición de equilibrio inicial. La distancia entre las espiras es la misma a lo largo del resorte. Si hacemos una representación esquemática de las espiras, podremos representarlas por trazos verticales. Si mantenemos la espira A en reposo, sujeta con la mano por ejemplo, y acercamos la espira B a A, la espira B sufre la acción simultánea de dos fuerzas recuperadoras que la empujan para que vuelva a su posición inicial. Al dejar libre B, como le hemos aportado una energía potencial mecánica, se mueve hacia la derecha, pero sobrepasa su posición inicial y se acerca a la espira C. Esta espira es entonces comprimida, mientras que B vuelve hacia su posición inicial. Pero C, que ha recibido energía mecánica, se desplaza hacia l a derecha, y así sucesivamente | ||
| + | |||
| + | Tomando nota de todas estas observaciones, concluiremos: | ||
| + | |||
| + | |||
<math>\Delta \mbox{P}</math> | <math>\Delta \mbox{P}</math> | ||
<math>\mbox{actualizando}</math> | <math>\mbox{actualizando}</math> | ||
Revisión de 09:01 3 dic 2007
El movimiento ondulatorio es la propagación de una perturbación en un medio elástico producida en uno cualquiera de sus puntos. El movimiento ondulatorio transporta o propaga energía sin que haya traslación de los puntos del medio.
Observaciones
a) Perturbación propagándose a lo largo de una cuerda
Imaginemos una cuerda mantenida horizontal a la que propinamos una sacudida en uno de sus extremos. Observamos que la deformación que hemos provocado se desplaza rápidamente a lo largo de la cuerda.
Marcamos sobre la cuerda un elemento de longitud 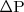 , y observamos los efectos de la sacudida sobre el mismo.
, y observamos los efectos de la sacudida sobre el mismo.
[Unparseable or potentially dangerous latex formula. Error 3 ]
Del movimiento que se genera en la cuerda podremos anotar las siguientes observaciones:
- - La perturbación tarda un tiempo en alcanzar el elemento
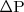 . Tiene que recorrer un tramo de cuerda hasta alcanzar
. Tiene que recorrer un tramo de cuerda hasta alcanzar 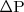 . Es decir alcanza
. Es decir alcanza 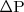 con cierto retraso con respecto al instante de la sacudida.
con cierto retraso con respecto al instante de la sacudida.
- - Cuando la perturbación alcanza
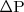 , éste es sometido inicialmente a la acción de una fuerza ascendente, elevando
, éste es sometido inicialmente a la acción de una fuerza ascendente, elevando 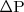 hasta alcanzar un máximo. Una vez alcanzado este máximo, se encuentra sometido a fuerzas ascendentes en el tramo que aún no lo ha alcanzado, y una fuerza descendente, ejercida por los elemento de cuerda precedentes, y que le hacen recuperar la forma inicial.
hasta alcanzar un máximo. Una vez alcanzado este máximo, se encuentra sometido a fuerzas ascendentes en el tramo que aún no lo ha alcanzado, y una fuerza descendente, ejercida por los elemento de cuerda precedentes, y que le hacen recuperar la forma inicial.
- - Por otra parte, el elemento
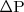 no se desplaza hacia los lados, sino que permanece en el plano vertical que se realizó la sacudida inicialmente. Diremos, como se verá más adelante, que está polarizada.
no se desplaza hacia los lados, sino que permanece en el plano vertical que se realizó la sacudida inicialmente. Diremos, como se verá más adelante, que está polarizada.
- - Si la cuerda está sujeta en el otro extremo, se producirá una reflexión, fenómeno que también se estudiará más adelante, pero siempre, todos los elementos de la cuerda se mantendrán en el mismo plano.
Una perturbación de estas características se denomina pulso y, en este caso, ha generado una onda transversal. La llamamos así porque el desplazamiento de cada punto perteneciente a 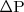 , mientras se encuentra sometido a la perturbación, es en todo instante perpendicular a la dirección de la propagación de la onda a lo largo de la cuerda.
, mientras se encuentra sometido a la perturbación, es en todo instante perpendicular a la dirección de la propagación de la onda a lo largo de la cuerda.
La onda es unidimensional puesto que se propaga en una sola dirección.
b) Perturbación sobre la superficie de un líquido.
Podemos rellenar de agua una bandeja poco profunda colocando en un lugar cualquiera de su superficie un tapón de corcho.
Si tocamos ligeramente con un punzón, se observará un círculo que irá haciéndose mayor. Cuando alcance la posición del corcho, se observará que éste realizará una oscilación vertical, pero no se trasladará sobre la superficie del agua. El movimiento del corcho nos pondrá en evidencia el movimiento de cada punto de la superficie del agua cuando le llega la perturbación. La onda generada será transversal y bidimensional puesto que se propaga en un plano.
c) Deformación que se propaga a lo largo de un resorte.
Sobre un resorte que hemos sujetado por sus extremos, manteniéndolo horizontal en la medida de lo posible, realizamos una deformación comprimiendo una parte del mismo. Inmediatamente después, soltamos, se observa que esa compresión se va propagando a lo largo del resorte.
El mismo efecto se observa si en lugar de comprimir las espiras, las separamos (decimos que realizamos una depresión o expansión)
Podemos hacer una representación esquemática de las espiras.
Consideremos que las espiras en ningún momento se yuxtaponen. Partimos de la posición de equilibrio inicial. La distancia entre las espiras es la misma a lo largo del resorte. Si hacemos una representación esquemática de las espiras, podremos representarlas por trazos verticales. Si mantenemos la espira A en reposo, sujeta con la mano por ejemplo, y acercamos la espira B a A, la espira B sufre la acción simultánea de dos fuerzas recuperadoras que la empujan para que vuelva a su posición inicial. Al dejar libre B, como le hemos aportado una energía potencial mecánica, se mueve hacia la derecha, pero sobrepasa su posición inicial y se acerca a la espira C. Esta espira es entonces comprimida, mientras que B vuelve hacia su posición inicial. Pero C, que ha recibido energía mecánica, se desplaza hacia l a derecha, y así sucesivamente
Tomando nota de todas estas observaciones, concluiremos:
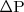
[Unparseable or potentially dangerous latex formula. Error 3 ]
Tweet


